
Binomial Theorem (Binomial Formula)
Some of the links below are affiliate links. As an Amazon Associate I earn from qualifying purchases. If you purchase through these links, it won't cost you any additional cash, but it will help to support my channel. Thank you! ►PRODUCT RECOMMENDATIONS https://www.amazon.com/shop/brithem
From playlist Probability

Algebra Ch 49: Binomial Theorem (1 of 18) What is the Binomial Theorem?
Visit http://ilectureonline.com for more math and science lectures! To donate: http://www.ilectureonline.com/donate https://www.patreon.com/user?u=3236071 We will learn binomial means an algebraic expression with 2 terms, and binomial theorem is a general solution to (a+b)^n=? where n is
From playlist ALGEBRA CH 49 THE BINOMIAL THEOREM

The Binomial Theorem | A-level Mathematics
Understanding the binomial theorem. Thanks for watching! This is applicable when the exponent of the binomial is a natural number. If the exponent is a fraction, you need a slightly different version of this theorem which is a topic for another video. ❤️ ❤️ ❤️ Support the channel ❤️
From playlist A-level Mathematics Revision
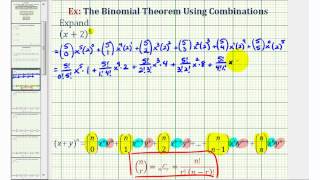
Ex 1: The Binomial Theorem Using Combinations
This provides a basic example of how to expand a binomial raised to a power using the binomial theorem. Site: http://mathispower4u.com
From playlist Using the Binomial Theorem / Combinations

Differential Equations | Abel's Theorem
We present Abel's Theorem with a proof. http://www.michael-penn.net
From playlist Differential Equations

What is the Binomial Theorem? (and How to Use It) | Algebra, Binomial Expansion, Summation Notation
What is the binomial theorem and how do we use it? We go over that, including a pretty gnarly binomial theorem example, in today’s math lesson! The binomial theorem is used to expand binomials raised to the power of positive integers. Expanding binomials that are raised to powers much gr
From playlist Probability Theory

SHM - 16/01/15 - Constructivismes en mathématiques - Frédéric Brechenmacher
Frédéric Brechenmacher (LinX, École polytechnique), « Effectivité et généralité dans la construction des grandeurs algébriques de Kronecker »
From playlist Les constructivismes mathématiques - Séminaire d'Histoire des Mathématiques

Tristan Riviere: The work of Louis Nirenberg on Partial Differential Equations
Original title of the lecture: "Exploring the unknown, the work of Louis Nirenberg on Partial Differential Equations" We had to shorten the title to fit Youtubes limitations of title length. Abastract: Partial differential equations are a central object in the mathematical modeling of na
From playlist Abel Lectures

Discrete Math II - 6.4.1 The Binomial Theorem
We start with a bit of review of sigma notation and some understanding of exactly what the binomial theorem is all about before jumping into the binomial theorem and its associated formula. We then take a look at a few typical applications of the binomial theorem by finding a binomial expa
From playlist Discrete Math II/Combinatorics (entire course)

A More General Binomial Theorem (Calculus Made Easy, pre Chapter 4)
#CalculusMadeEasy We're used to having positive integers as exponents with the Binomial Theorem. As a prelude to Chapter 4 of Thompson's "Calculus Made Easy," (Get it free: https://bit.ly/EasyCalculus) we need to tweak the Binomial Theorem, for fractional and negative exponents. The Binomi
From playlist Binomial Theorem

Sebastian Noelle: Systems of conservation laws
Programme for the Abel Lectures 2005: 1. "Abstract Phragmen-Lindelöf theorem & Saint Venant’s principle" by Abel Laureate 2005 Peter D. Lax, New York University 2. "Systems of conservation laws" by Professor Sebastian Noelle, CMA Oslo/ RWTH Aachen 3. "Hyperbolic equations and spectral g
From playlist Abel Lectures

Math 131 Spring 2022 042722 Properties of Analytic Functions, continued
Recall: analytic functions are infinitely (term-by-term) differentiable. Relation of coefficients and values of derivatives. Remark: analytic functions completely determined by values on an arbitrarily small interval. Analytic functions: convergence at an endpoint implies continuity the
From playlist Math 131 Spring 2022 Principles of Mathematical Analysis (Rudin)

Normal distribution excel exercise | Probability and Statistics | Khan Academy
Courses on Khan Academy are always 100% free. Start practicing—and saving your progress—now: https://www.khanacademy.org/math/statistics-probability/modeling-distributions-of-data/more-on-normal-distributions/v/normal-distribution-excel-exercise (Long-26 minutes) Presentation on spreadsh
From playlist Inferential statistics | Probability and Statistics | Khan Academy

8ECM Plenary Lecture: Umberto Zannier
From playlist 8ECM Plenary Lectures

The Abel Prize announcement 2020 — Hillel Furstenberg & Gregory Margulis
0:50 The Abel Prize announced by Hans Petter Graver, President of The Norwegian Academy of Science and Letters 1:37 Citation by Hans Munthe-Kaas, Chair of the Abel committee 9:28 Popular presentation of the prize winners work by Alex Bellos, British writer, and science communicator 16:21 I
From playlist Gregory Margulis

Differential Equations | Application of Abel's Theorem Example 2
We give an example of applying Abel's Theorem to construct a second solution to a differential equation given one solution. www.michael-penn.net
From playlist Differential Equations

6,000,000 and Abel Prize - Numberphile
Endre Szemerédi wins the mathematics equivalent of the Nobel Prize - the 2012 Abel Prize. He wins 6,000,000 Norwegian Kroner for his troubles. More links & stuff in full description below ↓↓↓ Featuring Dr David Hodge and Dr James Grime. A note from James about a mistake he made discussi
From playlist Related videos on other channels

Abel Prize award ceremony 2021
The ceremony honours both the 2020-winners, Hillel Furstenberg and Gregory Margulis, and the 2021-winners, Avi Wigderson and László́ Lovász. 0:30 Haddy N'jie sings Feeling Good 3:18 Welcome by Master of ceremonies, Haddy N'jie 4:46 On the nomination process and the work of the Abel Prize
From playlist Gregory Margulis

Discrete Math - 6.4.1 The Binomial Theorem
This is an introduction to the Binomial Theorem which allows us to use binomial coefficients to quickly determine the expansion of binomial expressions. Pascals Triangle is also covered. Textbook: Rosen, Discrete Mathematics and Its Applications, 7e Playlist: https://www.youtube.com/pla
From playlist Discrete Math I (Entire Course)
