
Reaching for Infinity Through Honeycombs – Roice Nelson
Pick any three integers larger than 2. We describe how to understand and draw a picture of a corresponding kaleidoscopic {p,q,r} honeycomb, up to and including {∞,∞,∞}.
From playlist G4G12 Videos

These sculptures are joint work with Roice Nelson. They are available from shapeways.com at http://shpws.me/oNgi, http://shpws.me/oqOx and http://shpws.me/orB8.
From playlist 3D printing

How to Construct a Dodecahedron
How the greeks constructed the Dodecahedron. Euclids Elements Book 13, Proposition 17. In geometry, a dodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. A regular dode
From playlist Platonic Solids
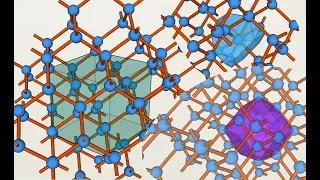
Three space-filling shapes hiding in the structure of diamond
Diamond is an arrangement of carbon atoms called the diamond cubic structure. As well as the cubes there are two other space-filling shapes that are found within it. In the unit cell I say "three more inside". It should of course be "four more inside". https://en.wikipedia.org/wiki/Diamo
From playlist Geometry

Canonical structures inside the Platonic solids III | Universal Hyperbolic Geometry 51
The dodecahedron is surely one of the truly great mathematical objects---revered by the ancient Greeks, Kepler, and many mathematicians since. Its symmetries are particularly rich, and in this video we look at how to see the five-fold and six-fold symmetries of this object via internal str
From playlist Universal Hyperbolic Geometry

Why do Bees build Hexagons? Honeycomb Conjecture explained by Thomas Hales
Mathematician Thomas Hales explains the Honeycomb Conjecture in the context of bees. Hales proved that the hexagon tiling (hexagonal honeycomb) is the most efficient way to maximise area whilst minimising perimeter. Interview with Oxford Mathematician Dr Tom Crawford. Produced by Tom Roc
From playlist Mathstars

Seven dots math puzzle solution
Here is the solution to my 7 dots and 6 triplets math puzzle: http://www.youtube.com/watch?v=LRrDIeDdRI8 I hope you enjoyed it! Next puzzle: http://www.youtube.com/watch?v=lGRqGLMWcns
From playlist Tricks and Math Puzzles answers

Particle distribution in a honeycomb maze with rounded cells
This simulation shows the particle distribution in a honeycomb maze, which was introduced in the video https://youtu.be/a3ICP1wQyR8 . The walls of each hexagonal cell are part of a same circle which is inscribed in the hexagon. As we have seen in the previous video, particles can spend lon
From playlist Illumination problem

7. Natural Honeycombs: Cork; Foams: Linear Elasticity
MIT 3.054 Cellular Solids: Structure, Properties and Applications, Spring 2015 View the complete course: http://ocw.mit.edu/3-054S15 Instructor: Lorna Gibson This session begins with a look at cork as a natural honeycomb structure, and covers properties of foams and some modeling. Licens
From playlist MIT 3.054 Cellular Solids: Structure, Properties and Applications, Spring 2015

Inverse problem by Abhinav Kumar
DISCUSSION MEETING SPHERE PACKING ORGANIZERS: Mahesh Kakde and E.K. Narayanan DATE: 31 October 2019 to 06 November 2019 VENUE: Madhava Lecture Hall, ICTS Bangalore Sphere packing is a centuries-old problem in geometry, with many connections to other branches of mathematics (number the
From playlist Sphere Packing - 2019

MIT 3.054 Cellular Solids: Structure, Properties and Applications, Spring 2015 View the complete course: http://ocw.mit.edu/3-054S15 Instructor: Lorna Gibson This session covers wood structure, micro-structure, stress-strain, honeycomb models, and bending. License: Creative Commons BY-NC
From playlist MIT 3.054 Cellular Solids: Structure, Properties and Applications, Spring 2015

An Introduction to Tensor Renormalization Group (Lecture 4) by Daisuke Kadoh
PROGRAM NONPERTURBATIVE AND NUMERICAL APPROACHES TO QUANTUM GRAVITY, STRING THEORY AND HOLOGRAPHY (HYBRID) ORGANIZERS: David Berenstein (University of California, Santa Barbara, USA), Simon Catterall (Syracuse University, USA), Masanori Hanada (University of Surrey, UK), Anosh Joseph (II
From playlist NUMSTRING 2022

Supersymmetry on the lattice: Geometry, Topology, and Spin Liquids by Simon Trebst
PROGRAM FRUSTRATED METALS AND INSULATORS (HYBRID) ORGANIZERS Federico Becca (University of Trieste, Italy), Subhro Bhattacharjee (ICTS-TIFR, India), Yasir Iqbal (IIT Madras, India), Bella Lake (Helmholtz-Zentrum Berlin für Materialien und Energie, Germany), Yogesh Singh (IISER Mohali, In
From playlist FRUSTRATED METALS AND INSULATORS (HYBRID, 2022)

Gallai-Edmonds Percolation by Kedar Damle
DISCUSSION MEETING : STATISTICAL PHYSICS OF COMPLEX SYSTEMS ORGANIZERS : Sumedha (NISER, India), Abhishek Dhar (ICTS-TIFR, India), Satya Majumdar (University of Paris-Saclay, France), R Rajesh (IMSc, India), Sanjib Sabhapandit (RRI, India) and Tridib Sadhu (TIFR, India) DATE : 19 December
From playlist Statistical Physics of Complex Systems - 2022

The Mysterious Architecture of the Universe - with J Richard Gott
J Richard Gott leads a journey through the history of our understanding of the Universe’s structure, and explains the ‘cosmic web’: the idea that our Universe is like a sponge made up of clusters of galaxies intricately connected by filaments of galaxies. Watch the Q&A here: https://youtu
From playlist Ri Talks

Monomer Percolation by Kedar Damle
PROGRAM FRUSTRATED METALS AND INSULATORS (HYBRID) ORGANIZERS Federico Becca (University of Trieste, Italy), Subhro Bhattacharjee (ICTS-TIFR, India), Yasir Iqbal (IIT Madras, India), Bella Lake (Helmholtz-Zentrum Berlin für Materialien und Energie, Germany), Yogesh Singh (IISER Mohali, In
From playlist FRUSTRATED METALS AND INSULATORS (HYBRID, 2022)
Román Orús: "News on tensor network simulations for quantum matter and beyond"
Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021 Workshop II: Tensor Network States and Applications "News on tensor network simulations for quantum matter and beyond" Román Orús - Donostia International Physics Center Abstract: In this talk I will make an
From playlist Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021

This shows a 3d print of a mathematical sculpture I produced using shapeways.com. This model is available at http://shpws.me/q0PF.
From playlist 3D printing

Tailoring Topological Phases: A Materials Perspective by Tanusri Saha-Dasgupta
DISCUSSION MEETING NOVEL PHASES OF QUANTUM MATTER ORGANIZERS: Adhip Agarwala, Sumilan Banerjee, Subhro Bhattacharjee, Abhishodh Prakash and Smitha Vishveshwara DATE: 23 December 2019 to 02 January 2020 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Recent theoretical and experimental
From playlist Novel Phases of Quantum Matter 2019
