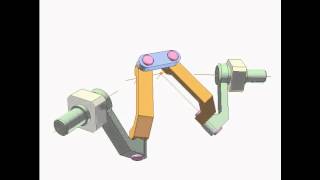
Modification of "Spherical 4R mechanism 2a" and "Spherical 4R mechanism 2b". Because it is a combination of two spherical 4R joints, angles between line connecting two joint centers and the shaft axles must be set equal to each other in order to get constant velocity.
From playlist Mechanisms

What is the 4th Dimension REALLY? - 4D Golf Devlog #2
A more practical explanation for those interested in exploring 4D spaces. For those not already familiar with basic 4D concepts, here's some videos I can recommend: "Visualizing 4D Geometry" https://www.youtube.com/watch?v=4URVJ3D8e8k "The things you'll find in higher dimensions" https:/
From playlist 4D Golf

Manifolds 1.3 : More Examples (Animation Included)
In this video, I introduce the manifolds of product manifolds, tori/the torus, real vectorspaces, matrices, and linear map spaces. This video uses a math animation for visualization. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : http://docdro.id/5koj5
From playlist Manifolds

What is a Manifold? Lesson 15: The cylinder as a quotient space
What is a Manifold? Lesson 15: The cylinder as a quotient space This lesson covers several different ideas on the way to showing how the cylinder can be described as a quotient space. Lot's of ideas in this lecture! ... too many probably....
From playlist What is a Manifold?

Manifolds #5: Tangent Space (part 1)
Today, we introduce the notion of tangent vectors and the tangent vector space at a point on a manifold.
From playlist Manifolds

4th dimension 'n stuff -- Day 5
alright, 4th dimension visualized! -- Watch live at https://www.twitch.tv/simuleios
From playlist 4d visualization
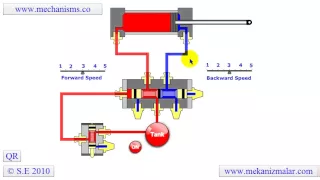
How five port four way valve works air - spring
http://www.mekanizmalar.com This video describes working principles of a five port four way valve. This valve's spool shift from natural position with air pressure and return to natural position by spring.
From playlist Pneumatic and Hydraulics

How five port four way valve works air - air
http://www.mekanizmalar.com This video shows working principle of five port four way valve. Left and right pilot ports have connection for pilot air.
From playlist Pneumatic and Hydraulics

Alice Chang: Conformal Geometry on 4-manifolds
Abstract: In this talk, I will report on the study of integral conformal invariants on 4-manifolds and applications to the study of topology and diffeomorphism type of a class of 4-manifolds. The key ingredient is the study of the integral of 2 of the Schouten tensor which is the part of i
From playlist Abel in... [Lectures]

Jack Calcut: Mazur and Jester 4-manifolds
Jack Calcut, Oberlin College Title: Mazur and Jester 4-manifolds Mazur and Po{\'e}naru constructed the first compact, contractible manifolds distinct from disks. More recently, Sparks modified Mazur's construction and defined Jester manifolds. Sparks used Jester manifolds to produce compac
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022

Jessica Purcell: Structure of hyperbolic manifolds - Lecture 2
Abstract: In these lectures, we will review what it means for a 3-manifold to have a hyperbolic structure, and give tools to show that a manifold is hyperbolic. We will also discuss how to decompose examples of 3-manifolds, such as knot complements, into simpler pieces. We give conditions
From playlist Topology

Lecture 4: VOA[M4] (Lecture 3) by Sergei Gukov
Program: Quantum Fields, Geometry and Representation Theory ORGANIZERS : Aswin Balasubramanian, Saurav Bhaumik, Indranil Biswas, Abhijit Gadde, Rajesh Gopakumar and Mahan Mj DATE & TIME : 16 July 2018 to 27 July 2018 VENUE : Madhava Lecture Hall, ICTS, Bangalore The power of symmetries
From playlist Quantum Fields, Geometry and Representation Theory

Emmy Noether Lecture: Conformal geometry on 4-manifolds — Sun-Yung Alice Chang — ICM2018
Conformal geometry on 4-manifolds Sun-Yung Alice Chang Abstract: In this talk, I will report on the study of a class of integral conformal invariants on 4-manifolds and applications to the study of topology and diffeomorphism type of a class of 4-manifolds. The key ingredient is the study
From playlist Special / Prizes Lectures

Compactness of conformally compact Einstein manifolds in dimension 4 - Alice Chang
Workshop on Geometric Functionals: Analysis and Applications Topic: Compactness of conformally compact Einstein manifolds in dimension 4 Speaker: Alice Chang Affiliation:Princeton University Date: March 4, 2019 For more video please visit http://video.ias.edu
From playlist Workshop on Geometric Functionals: Analysis and Applications

Hsueh-Yung Lin: On the existence of algebraic approximations of compact Kähler manifolds
Abstract: Let X be a compact Kähler manifold. The so-called Kodaira problem asks whether X has arbitrarily small deformations to some projective varieties. While Kodaira proved that such deformations always exist for surfaces. Starting from dimension 4, there are examples constructed by Vo
From playlist Analysis and its Applications

This lecture was held by Abel Laureate John Milnor at The University of Oslo, May 25, 2011 and was part of the Abel Prize Lectures in connection with the Abel Prize Week celebrations. Program for the Abel Lectures 2011 1. "Spheres" by Abel Laureate John Milnor, Institute for Mathematical
From playlist Abel Lectures

Maggie Miller - The Price twist via trisections
June 20, 2018 - This talk was part of the 2018 RTG mini-conference Low-dimensional topology and its interactions with symplectic geometry The Price twist is a surgery operation on an RP^2 in a 4-manifold that may change the smooth structure of the 4-manifold. Akbulut showed that this ope
From playlist 2018 RTG mini-conference on low-dimensional topology and its interactions with symplectic geometry I
Overview of gauge theory and submanifold geometry on G_2 manifolds - Simon Donaldson [2014]
Name: Simon Donaldson Event: Program: G2 manifolds Event URL: view webpage Title: Overview of gauge theory and submanifold geometry on G_2 manifolds, I Date: 2014-08-19 @3:30 PM
From playlist Mathematics

Conformal gap theorems of $S^4$ and $CP^2$ - Alice Chang [2017]
slides for this talk: https://drive.google.com/file/d/1d6Vzy5Rp3s2vZe0CWfr7nnwK5kG0RO_C/view?usp=sharing Name: Alice Chang Event: Workshop: Geometry of Manifolds Event URL: view webpage Title: Conformal gap theorems of $S^4$ and $CP^2$ Date: 2017-10-25 @9:30 AM Location: 102 Download the
From playlist Mathematics

Jessica Purcell: Structure of hyperbolic manifolds - Lecture 3
Abstract: In these lectures, we will review what it means for a 3-manifold to have a hyperbolic structure, and give tools to show that a manifold is hyperbolic. We will also discuss how to decompose examples of 3-manifolds, such as knot complements, into simpler pieces. We give conditions
From playlist Topology