
Zagier's conjecture on zeta(F,4) - Alexander Goncharov
Workshop on Motives, Galois Representations and Cohomology Around the Langlands Program Topic: Zagier's conjecture on zeta(F,4) Speaker: Alexander Goncharov Affiliation: Yale University; Member, School of Mathematics Date: November 10, 2017 For more videos, please visit http://video.ias.
From playlist Mathematics

Rahim Moosa: Around Jouanolou-type theorems
Abstract: In the mid-90’s, generalising a theorem of Jouanolou, Hrushovski proved that if a D-variety over the constant field C has no non-constant D-rational functions to C, then it has only finitely many D-subvarieties of codimension one. This theorem has analogues in other geometric con
From playlist Combinatorics

Calculus - The Fundamental Theorem, Part 1
The Fundamental Theorem of Calculus. First video in a short series on the topic. The theorem is stated and two simple examples are worked.
From playlist Calculus - The Fundamental Theorem of Calculus

Silvia Steila: An overview over least fixed points in weak set theories
Given a monotone function on a complete lattice the least fixed point is defined as the minimum among the fixed points. Tarski Knaster Theorem states that every monotone function on a complete lattice has a least fixed point. There are two standard proofs of Tarski Knaster Theorem. The f
From playlist Workshop: "Proofs and Computation"

Monotonicity of the Riemann zeta function and related functions - P Zvengrowski [2012]
General Mathematics Seminar of the St. Petersburg Division of Steklov Institute of Mathematics, Russian Academy of Sciences May 17, 2012 14:00, St. Petersburg, POMI, room 311 (27 Fontanka) Monotonicity of the Riemann zeta function and related functions P. Zvengrowski University o
From playlist Number Theory
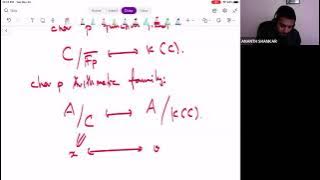
Ananth Shankar, Picard ranks of K3 surfaces and the Hecke orbit conjecture
VaNTAGe Seminar, November 23, 2021
From playlist Complex multiplication and reduction of curves and abelian varieties
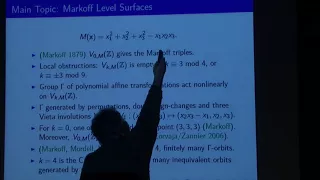
Integral points on Markoff-type cubic surfaces - Amit Ghosh
Special Seminar Topic: Integral points on Markoff-type cubic surfaces Speaker: Amit Ghosh Affiliation: Oklahoma State University Date: December 8, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics
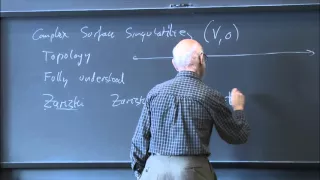
Geometry of complex surface singularities and 3-manifolds - Neumann
Geometric Structures on 3-manifolds Topic: Geometry of complex surface singularities and 3-manifolds Speaker: Walter Neumann Date: Tuesday, January 26 I will talk about bilipschitz geometry of complex algebraic sets, focusing on the local geometry in dimension 2 (complex surface singulari
From playlist Mathematics

On Zaremba's Conjecture on Continued Fractions - Jean Bourgain
Jean Bourgain Institute for Advanced Study February 14, 2012 Zaremba's 1971 conjecture predicts that every integer appears as the denominator of a finite continued fraction whose partial quotients are bounded by an absolute constant. We confirm this conjecture for a set of density one. Fo
From playlist Mathematics

Weil conjectures 6: etale cohomology of a curve
We give an overview of how to calculate the etale cohomology of a nonsinguar projective curve over an algebraically closed field with coefficients Z/nZ with n invertible. We simply assume a lot of properties of etale cohomology without proving (or even defining) them.
From playlist Algebraic geometry: extra topics

Introduction to additive combinatorics lecture 1.8 --- Plünnecke's theorem
In this video I present a proof of Plünnecke's theorem due to George Petridis, which also uses some arguments of Imre Ruzsa. Plünnecke's theorem is a very useful tool in additive combinatorics, which implies that if A is a set of integers such that |A+A| is at most C|A|, then for any pair
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

Introduction to additive combinatorics lecture 10.8 --- A weak form of Freiman's theorem
In this short video I explain how the proof of Freiman's theorem for subsets of Z differs from the proof given earlier for subsets of F_p^N. The answer is not very much: the main differences are due to the fact that cyclic groups of prime order do not have lots of subgroups, so one has to
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

The Fundamental Theorem of Calculus and How to Use it
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys The Fundamental Theorem of Calculus and How to Use it
From playlist Calculus 1

From continuous rational to regulous functions – Krzysztof Kurdyka & Wojciech Kucharz – ICM2018
Algebraic and Complex Geometry Invited Lecture 4.6 From continuous rational to regulous functions Krzysztof Kurdyka & Wojciech Kucharz Abstract: Let X be an algebraic set in ℝⁿ. Real-valued functions, defined on subsets of X, that are continuous and admit a rational representation have s
From playlist Algebraic & Complex Geometry

Complexes of tori and rational points on homogeneous (...) - Harari - Workshop 1 - CEB T2 2019
David Harari (Université Paris Sud) / 20.05.2019 Complexes of tori and rational points on homogeneous spaces over a function field We explain new arithmetic duality theorems for finite group schemes and 2-term complexes of tori defined over a global field of positive characteristic. We
From playlist 2019 - T2 - Reinventing rational points

Patrick Ingram, The critical height of an endomorphism of projective space
VaNTAGe seminar on June 9, 2020. License: CC-BY-NC-SA. Closed captions provided by Matt Olechnowicz
From playlist Arithmetic dynamics

Yohann Genzmer : The Zariski problem for homogeneous and quasi-homogeneous curves
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

Commensurators of thin Subgroups by Mahan M. J.
PROGRAM SMOOTH AND HOMOGENEOUS DYNAMICS ORGANIZERS: Anish Ghosh, Stefano Luzzatto and Marcelo Viana DATE: 23 September 2019 to 04 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Ergodic theory has its origins in the the work of L. Boltzmann on the kinetic theory of gases.
From playlist Smooth And Homogeneous Dynamics
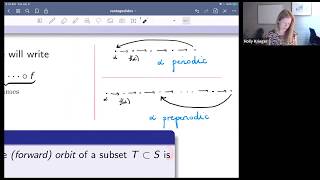
Holly Krieger, Equidistribution and unlikely intersections in arithmetic dynamics
VaNTAGe seminar on May 26, 2020. License: CC-BY-NC-SA. Closed captions provided by Marley Young.
From playlist Arithmetic dynamics

Set Theory (Part 2): ZFC Axioms
Please feel free to leave comments/questions on the video and practice problems below! In this video, I introduce some common axioms in set theory using the Zermelo-Fraenkel w/ choice (ZFC) system. Five out of nine ZFC axioms are covered and the remaining four will be introduced in their
From playlist Set Theory by Mathoma