
What is the difference between convex and concave polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Asymptotes and intercepts of the reciprocal function
👉 Learn how to find the vertical/horizontal asymptotes of a function. An asymptote is a line that the graph of a function approaches but never touches. The vertical asymptote is a vertical line that the graph of a function approaches but never touches. To find the vertical asymptote(s) of
From playlist Find the Asymptotes of Rational Functions

When do we have an oblique, slant asymptote for a rational function
👉 Learn all about asymptotes of a rational function. A rational function is a function, having a variable in the denominator. An asymptote is a line that the graph of a function approaches but never touches. There are the vertical, the horizontal and the slant/oblique asymptotes. The ver
From playlist Asymptotes of Rational Functions | Learn About
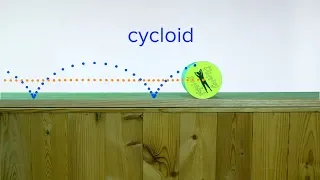
#Cycloid: A curve traced by a point on a circle rolling in a straight line. (A preview of this Sunday's video.)
From playlist Miscellaneous

How to find the Asymptotes and Intercepts of a Rational Function
👉 Learn how to find the vertical/horizontal asymptotes of a function. An asymptote is a line that the graph of a function approaches but never touches. The vertical asymptote is a vertical line that the graph of a function approaches but never touches. To find the vertical asymptote(s) of
From playlist Find the Asymptotes of Rational Functions

What is the difference between convex and concave
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons
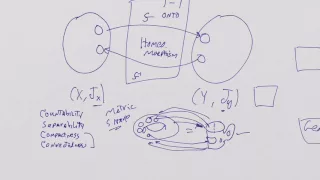
What is a Manifold? Lesson 5: Compactness, Connectedness, and Topological Properties
The last lesson covering the topological prep-work required before we begin the discussion of manifolds. Topics covered: compactness, connectedness, and the relationship between homeomorphisms and topological properties.
From playlist What is a Manifold?

Lie Groups and Lie Algebras: Lesson 36 - Review of continuity and homeomorphisms
Lie Groups and Lie Algebras: Lesson 36 - Review of continuity and homeomorphisms This is a review lesson regarding the topological definition of continuity, homeomorphism, and topological properties. This is important because the Fundamental group of a topological space is a topological
From playlist Lie Groups and Lie Algebras

Overivew of Rational Functions
👉 Learn all about asymptotes of a rational function. A rational function is a function, having a variable in the denominator. An asymptote is a line that the graph of a function approaches but never touches. There are the vertical, the horizontal and the slant/oblique asymptotes. The ver
From playlist Asymptotes of Rational Functions | Learn About

What is a Manifold? Lesson 15: The cylinder as a quotient space
What is a Manifold? Lesson 15: The cylinder as a quotient space This lesson covers several different ideas on the way to showing how the cylinder can be described as a quotient space. Lot's of ideas in this lecture! ... too many probably....
From playlist What is a Manifold?

Algebraic Topology 1.5 : Covering Maps and the Fundamental Group of the Circle
In this video, I introduce what covering maps are, their property of lifting maps, the construction of unique lifts of paths, and then prove that the fundamental group of the circle is isomorphic to the integers using those lifts. Translate This Video : Notes : None yet Patreon : https://
From playlist Topology

Barcodes for Hamiltonian homeomorphisms of surfaces -Benoît Joly
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Topic: Barcodes for Hamiltonian homeomorphisms of surfaces Speaker: Benoît Joly Affiliation: Ruhr-Universität Bochum Date: March 25, 2022 In this talk, we will study the Floer Homology barcodes from a dynamical poin
From playlist Mathematics

Homeomorphisms and Homotopy Equivalences [Henry Adams]
We give a brief introduction to homeomorphisms, homotopy equivalences, and the difference between them. These notions describe when two shapes are described to be "the same" to a topologist. his tutorial was contributed as part of the WinCompTop+AATRN Tutorial-a-thon in Spring 2021: https
From playlist Tutorial-a-thon 2021 Spring

MAST30026 Lecture 7: Constructing topological spaces (Part 3)
Today's lecture was all about examples, constructed using the disjoint union, quotient and pushouts from last lecture. These examples includes the torus, Mobius band, and finally arbitrary CW complexes. Lecture notes: http://therisingsea.org/notes/mast30026/lecture7.pdf The class webpage:
From playlist MAST30026 Metric and Hilbert spaces

Sanjay Mishra: Preservation of Properties during Topological Equivalence of Function Space
Sanjay Mishra, Lovely Professional University Title: Preservation of Properties during Topological Equivalence of Function Space The study of convergence of sequence of functions is the most important and active area of research in theoretical mathematics that solve several problems of app
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Horizontal and Vertical asymptotes of rational functions
👉 Learn how to find the vertical/horizontal asymptotes of a function. An asymptote is a line that the graph of a function approaches but never touches. The vertical asymptote is a vertical line that the graph of a function approaches but never touches. To find the vertical asymptote(s) of
From playlist Find the Asymptotes of Rational Functions

Metric Spaces - Lectures 7 & 8: Oxford Mathematics 2nd Year Student Lecture
For the first time we are making a full Oxford Mathematics Undergraduate lecture course available. Ben Green's 2nd Year Metric Spaces course is the first half of the Metric Spaces and Complex Analysis course. This is the 4th of 11 videos. The course is about the notion of distance. You ma
From playlist Oxford Mathematics Student Lectures - Metric Spaces

Identifying vertical, horizontal asymptotes and holes
👉 Learn how to find the vertical/horizontal asymptotes of a function. An asymptote is a line that the graph of a function approaches but never touches. The vertical asymptote is a vertical line that the graph of a function approaches but never touches. To find the vertical asymptote(s) of
From playlist Find the Asymptotes of Rational Functions

Geometry of Surfaces - Topological Surfaces Lecture 4 : Oxford Mathematics 3rd Year Student Lecture
This is the fourth of four lectures from Dominic Joyce's 3rd Year Geometry of Surfaces course. The four lectures cover topological surfaces and conclude with a big result, namely the classification of surfaces. This lecture covers connected sums, orientations, and finally the classificatio
From playlist Oxford Mathematics Student Lectures - Geometry of Surfaces