
Physical Science 4.4a - The Wheel and Axle
An explanation of the simple machine known as the wheel and axle. The mechanical advantage and the trade off between force and distance is discussed in this and in the following videos.
From playlist Physical Science Chapter 4

Trigonometry - Working with linear and angular speed
When working with wheels its important to recognize that there is a connection between linear and angular speed. This video will show a few example on using the formula v = rw for finding either linear speed or angular speed. Near the end we also cover how to covert unit which is useful
From playlist Trigonometry

AWESOME Physics demonstrations. Wheel race (explaining simply)!
The concept of moment of inertia is demonstrated by rolling different bodies down an inclined plane (explaining simply).
From playlist MECHANICS

THE MAKING(English Version) (314)The Making of Steel Balls
This edition of the series of programs explaining the technology used to produce items that are familiar in our daily life features ‘Steel Balls’. A bicycle wheel spins smoothly because the wheel axle contains ball bearings. The steel balls inside the ball bearing must be close to perfectl
From playlist Engineering

The Perfect Road for a Square Wheel and How to Design It
How do you design a road that a square wheel will roll smoothly over? And what about other wheel shapes? How do you even approach such a problem? =Chapters= 0:00 - Intro 1:36 - The Dynamics of Rolling 4:05 - Vertical Alignment Property 7:16 - Stationary Rim Property 8:29 - Describing the
From playlist The Wonderful World of Weird Wheels

Physics 11.1 Rigid Body Rotation (4 of 10) Calculating Acceleration & Friction of a Car Tire
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain and calculate the acceleration and friction of the tire of a car.
From playlist PHYSICS 11 ROTATIONAL MOTION

Physics, Torque (6 of 13) Compound Wheel
Shows how to calculate the individual torques and net torque produced by forces applied to a compound wheel. Torque is a rotating force. It is a measure of how much force is acting on an object that causes the object to rotate. The object will rotate about an axis, which is called the piv
From playlist Torque and Static Equilibrium

This shows an small game that illustrates the concept of a vector. The clip is from the book "Immersive Linear Algebra" at http://www.immersivemath.com
From playlist Chapter 2 - Vectors

A Beautiful Algorithm for the Primes
What's the fastest algorithm for generating the prime sequence? Watch a frat bro hunch over a notebook and find out! . . . Walkthrough (pause, then use “,” and “.” keys to step): https://www.youtube.com/watch?v=GxgGMwLfTjE&t=4s Computing the primes up to 40,000 (also pause and use "," and
From playlist Summer of Math Exposition 2 videos

Francis BROWN - Graph Complexes, Invariant Differential Forms and Feynman integrals
Kontsevich introduced the graph complex GC2 in 1993 and raised the problem of determining its cohomology. This problem is of renewed importance following the recent work of Chan-Galatius-Payne, who related it to the cohomology of the moduli spaces Mg of curves of genus g. It is known by Wi
From playlist Algebraic Structures in Perturbative Quantum Field Theory: a conference in honour of Dirk Kreimer's 60th birthday

AWESOME Bicycle wheel gyroscope (science experiments)
Physics (la physique)(science experiments)
From playlist MECHANICS

Bootstrapping the lattice Yang-Mills theory by Zechuan Zheng
PROGRAM NONPERTURBATIVE AND NUMERICAL APPROACHES TO QUANTUM GRAVITY, STRING THEORY AND HOLOGRAPHY (HYBRID) ORGANIZERS: David Berenstein (University of California, Santa Barbara, USA), Simon Catterall (Syracuse University, USA), Masanori Hanada (University of Surrey, UK), Anosh Joseph (II
From playlist NUMSTRING 2022

Donald Hoffman on Consciousness and Conscious Agents | Closer To Truth Chats
Donal Hoffman discusses his theory of consciousness and conscious agents, and how this theory affects everything from artificial intelligence to alien life and the Fermi Paradox. Donald Hoffman's Website: http://www.cogsci.uci.edu/~ddhoff/ Follow Donald Hoffman on Twitter @donalddhoffman
From playlist Closer To Truth Chats

Extracting Eersatile Active Particle Dynamics from a Self-Propelled Programmable... by Nitin Kumar
DISCUSSION MEETING 8TH INDIAN STATISTICAL PHYSICS COMMUNITY MEETING ORGANIZERS: Ranjini Bandyopadhyay (RRI, India), Abhishek Dhar (ICTS-TIFR, India), Kavita Jain (JNCASR, India), Rahul Pandit (IISc, India), Samriddhi Sankar Ray (ICTS-TIFR, India), Sanjib Sabhapandit (RRI, India) and Prer
From playlist 8th Indian Statistical Physics Community Meeting-ispcm 2023

Spin Until You Lose - Probability Riddle
You spin a wheel and it randomly lands on $1, $2, or END. If you land on $1 or $2, you bank the money and spin the wheel again. You keep spinning until you land on END, at which point you cash out the money you banked. How much do you expect to win on average? What if the wheel has values
From playlist Statistics And Probability

Falling cat demonstrations go sour by Andy Ruina
COLLOQUIUM : FALLING CAT DEMONSTRATIONS GO SOUR SPEAKER: Andy Ruina (Cornell University, US) DATE: Mon, 25 April 2022, 15:30 to 17:00 VENUE: Online and Ramanujan Lecture Hall ABSTRACT There are two classes of interesting, at least to me, physical behavior that follow from the impossibi
From playlist ICTS Colloquia

Matrix Models, Gauge-Gravity Duality, and Simulations on the Lattice (Lecture 4) by Georg Bergner
PROGRAM NONPERTURBATIVE AND NUMERICAL APPROACHES TO QUANTUM GRAVITY, STRING THEORY AND HOLOGRAPHY (HYBRID) ORGANIZERS: David Berenstein (University of California, Santa Barbara, USA), Simon Catterall (Syracuse University, USA), Masanori Hanada (University of Surrey, UK), Anosh Joseph (II
From playlist NUMSTRING 2022

Why is a bicycle easier to balance at speed? | James May's Q&A | Head Squeeze
Why is riding a bike at speed easier than falling off one? Subscribe: http://bit.ly/SubscribeToEarthLab Gyroscopic force: http://www.howstuffworks.com/gyroscope1.htm Longest ramp jump on a mini bike: http://www.guinnessworldrecords.com/world-records/4000/longest-ramp-jump-on-a-mini-bike-(
From playlist James May's Q&A
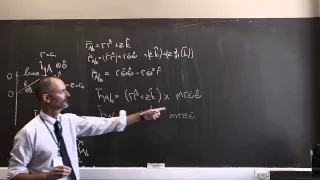
15 Angular momentum and torque example problem 1 part 2
Part 2 of the example problem showing what a difference a reference point makes to angular momentum and torque.
From playlist Life Science Math: Vectors

Ohad Kammar: An introduction to statistical modelling semantics with higher-order measure theory
HYBRID EVENT Recorded during the meeting "Logic of Probabilistic Programming" February 04, 2022 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audiov
From playlist Probability and Statistics