
What is an integral and it's parts
👉 Learn about integration. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which the upper and the lower li
From playlist The Integral

Definite Integral Using Limit Definition
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definite Integral Using Limit Definition. In this video we compute a definite integral using the limit definition.
From playlist Calculus
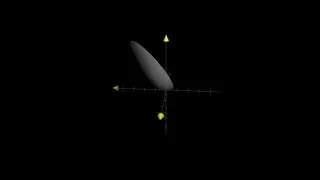
Region between x^2+y^2 and 2x+y+1
From playlist Triple integrals
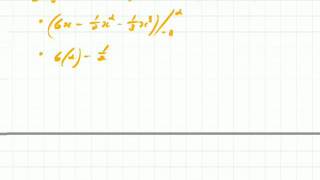
Integration 4 The Definite Integral Part 3 Example 1
An example using the definite integral.
From playlist Integration

Free ebook http://tinyurl.com/EngMathYT How to integrate over 2 curves. This example discusses the additivity property of line integrals (sometimes called path integrals).
From playlist Engineering Mathematics

Differential Isomorphism and Equivalence of Algebraic Varieties Board at 49:35 Sum_i=1^N 2/(x-phi_i(y,t))^2
From playlist Fall 2017

David Zywina, Computing Sato-Tate and monodromy groups.
VaNTAGe seminar on May 5, 2020. License: CC-BY-NC-SA Closed captions provided by Jun Bo Lau.
From playlist The Sato-Tate conjecture for abelian varieties

Yang Shi: Normalizer theory of Coxeter groups and discrete integrable systems
Abstract: Formulation of the Painleve equations and their generalisations as birational representations of affine Weyl groups provides us with an elegant and efficient way to study these highly transcendental, nonlinear equations. In particular, it is well-known that discrete evolutions of
From playlist Integrable Systems 9th Workshop

Transport in topological junctions by Krishnendu Sengupta
Program The 2nd Asia Pacific Workshop on Quantum Magnetism ORGANIZERS: Subhro Bhattacharjee, Gang Chen, Zenji Hiroi, Ying-Jer Kao, SungBin Lee, Arnab Sen and Nic Shannon DATE: 29 November 2018 to 07 December 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Frustrated quantum magne
From playlist The 2nd Asia Pacific Workshop on Quantum Magnetism

Math 139 Fourier Analysis Lecture 13: Weyl's equidistribution theorem
Weyl's equidistribution theorem: definition of equidistributed seqeunce; statement of theorem; rephrasal in terms of analysis; main lemma; proof of theorem; observations
From playlist Course 8: Fourier Analysis

Topology and the Electromagnetic Responses of Quantum Materials by Joel E. Moore
ICTS at Ten ORGANIZERS: Rajesh Gopakumar and Spenta R. Wadia DATE: 04 January 2018 to 06 January 2018 VENUE: International Centre for Theoretical Sciences, Bengaluru This is the tenth year of ICTS-TIFR since it came into existence on 2nd August 2007. ICTS has now grown to have more tha
From playlist ICTS at Ten
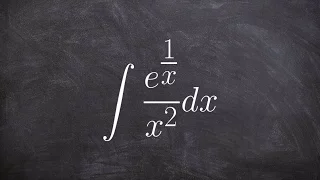
How to integrate exponential expression with u substitution
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

What is the constant rule of integration
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

Weyl groups, and their generalizations in, enumerative geometry II - Okounkov
Hermann Weyl Lectures Topic: Weyl groups, and their generalizations in, enumerative geometry II Speaker: Andrei Okounkov Date: Wednesday, March 16 These lectures will be about enumerative K-theory of curves (and more general 1-dimensional sheaves) in algebraic threefolds. In the firs
From playlist Hermann Weyl Lectures
Weyl groups, and their generalizations, in enumerative geometry I - Andrei Okounkov
Hermann Weyl Lectures Topic: Weyl groups, and their generalizations, in enumerative geometry I Speaker: Andrei Okounkov Date: Tuesday, March 15 These lectures will be about enumerative K-theory of curves (and more general 1-dimensional sheaves) in algebraic threefolds. In the first lec
From playlist Hermann Weyl Lectures

Use the FTOC to evaluate the integral
Keywords 👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as indefinite integral or as a definite integral. A definite integral is an integral in
From playlist Evaluate Integrals

Surface states and arcless angles in twisted Weyl semi-metals by Ganpathy Murthy
DISCUSSION MEETING NOVEL PHASES OF QUANTUM MATTER ORGANIZERS: Adhip Agarwala, Sumilan Banerjee, Subhro Bhattacharjee, Abhishodh Prakash and Smitha Vishveshwara DATE: 23 December 2019 to 02 January 2020 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Recent theoretical and experimental
From playlist Novel Phases of Quantum Matter 2019

To learn to think like a scientist check out http://Brilliant.org/SpaceTime PBS Member Stations rely on viewers like you. To support your local station, go to: http://to.pbs.org/DonateSPACE Check out the new Space Time Merch Store! https://pbsspacetime.com/ Support Space Time on Patreo
From playlist Understanding the Holographic Universe

Integration 4 The Definite Integral Part 2
Working through an example of the definite integral
From playlist Integration
