
Lagrange Multipiers: Find the Max and Min of a Function of Two Variables
This video explains how to use Lagrange Multipliers to maximum and minimum a function under a given constraint. The results are shown in using level curves. http://mathispower4u.com
From playlist Lagrange Multipliers

Ex: Solve a Bernoulli Differential Equation Using Separation of Variables
This video explains how to solve a Bernoulli differential equation. http://mathispower4u.com
From playlist Bernoulli Differential Equations
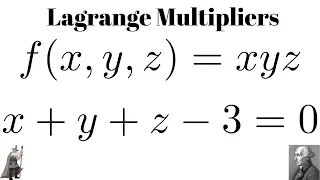
Lagrange Multipliers Maximum of f(x, y, z) = xyz subject to x + y + z - 3 = 0
Lagrange Multipliers Maximum of f(x, y, z) = xyz subject to x + y + z - 3 = 0
From playlist Calculus 3

Ex: Solve a Bernoulli Differential Equation Using an Integrating Factor
This video explains how to solve a Bernoulli differential equation. http://mathispower4u.com
From playlist Bernoulli Differential Equations
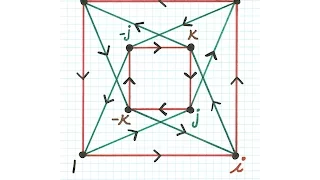
Euler's Formula for the Quaternions
In this video, we will derive Euler's formula using a quaternion power, instead of a complex power, which will allow us to calculate quaternion exponentials such as e^(i+j+k). If you like quaternions, this is a pretty neat formula and a simple generalization of Euler's formula for complex
From playlist Math
Standard and Nonstandard Comparisons of Relative Trace Formulas - Yiannis Sakellaridis
Yiannis Sakellaridis Rutgers, The State University of New Jersey March 1, 2013 The trace formula has been the most powerful and mainstream tool in automorphic forms for proving instances of Langlands functoriality, including character relations. Its generalization, the relative trace formu
From playlist Mathematics

Wave-front set of some representations... of the group SO(2n+1) - Jean-Loup Waldspurger
Workshop on Representation Theory and Analysis on Locally Symmetric Spaces Topic: Wave-front set of some representations of unipotent reduction of the group SO(2n+1) Speaker: Jean-Loup Waldspurger Affiliation: Univeristy of Jussieu Date: March 5, 2018 For more videos, please visit http:/
From playlist Mathematics

On the Fourier coefficients of a Cohen-Eisenstein series by Srilakshmi Krishnamoorthy
12 December 2016 to 22 December 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore The Birch and Swinnerton-Dyer conjecture is a striking example of conjectures in number theory, specifically in arithmetic geometry, that has abundant numerical evidence but not a complete general solution.
From playlist Theoretical and Computational Aspects of the Birch and Swinnerton-Dyer Conjecture

Leibniz formula for computing determinants | Lecture 30 | Matrix Algebra for Engineers
How to compute the determinant using the Leibniz formula (big formula). Join me on Coursera: https://www.coursera.org/learn/matrix-algebra-engineers Lecture notes at http://www.math.ust.hk/~machas/matrix-algebra-for-engineers.pdf Subscribe to my channel: http://www.youtube.com/user/jcha
From playlist Matrix Algebra for Engineers

Raphaël Beuzart-Plessis: The local Gan-Gross-Prasad conjecture for unitary groups
Abstract: The local Gan-Gross-Prasad conjectures concern certain branching or restriction problems between representations of real or p-adic Lie groups. In its simplest form it predicts certain multiplicity-one results for "extended" L-packets. In a recent series of papers, Waldspurger has
From playlist Jean-Morlet Chair - Prasad/Heiermann

Lagrange Multipliers Maximize f(x,y) = 2x + 2xy + y subject to 2x + y = 100
Lagrange Multipliers Maximize f(x,y) = 2x + 2xy + y subject to 2x + y = 100
From playlist Calculus 3

Rank optimality for the Burer-Monteiro factorization - Waldspurger - Workshop 3 - CEB T1 2019
Irène Waldspurger (CNRS and Paris-Dauphine) / 03.04.2019 Rank optimality for the Burer-Monteiro factorization In the last decades, semidefinite programs have emerged as a a powerful way to solve difficult combinatorial optimization problems in polynomial time. Unfortunately, they are di
From playlist 2019 - T1 - The Mathematics of Imaging

Euler's formulas, Rodrigues' formula
In this video I proof various generalizations of Euler's formula, including Rodrigues' formula and explain their 3 dimensional readings. Here's the text used in this video: https://gist.github.com/Nikolaj-K/eaaa80861d902a0bbdd7827036c48af5
From playlist Algebra

Illustrates the solution of a Bernoulli first-order differential equation. Free books: http://bookboon.com/en/differential-equations-with-youtube-examples-ebook http://www.math.ust.hk/~machas/differential-equations.pdf
From playlist Differential Equations with YouTube Examples

Shou-Wu Zhang: Congruent number problem and BSD conjecture
Abstract : A thousand years old problem is to determine when a square free integer n is a congruent number ,i,e, the areas of right angled triangles with sides of rational lengths. This problem has a some beautiful connection with the BSD conjecture for elliptic curves En:ny2=x3−x. In fact
From playlist Jean-Morlet Chair - Research Talks - Prasad/Heiermann

An Analogue of the Ichino-Ikeda Conjecture for... coefficients of the Metaplectic Group - Erez Lapid
Erez Lapid Hebrew University of Jerusalem and Weizmann Institute of Science March 14, 2013 A few years ago Ichino-Ikeda formulated a quantitative version of the Gross-Prasad conjecture, modeled after the classical work of Waldspurger. This is a powerful local-to-global principle which is
From playlist Mathematics

Math Park - 03/02/2018 - Irène WALDSPURGER - MINIMISATION DE FONCTIONS CONVEXES
Dans cet exposé, nous nous intéresserons à un problème apparemment basique : comment trouver la valeur minimale d'une fonction à valeurs réelles (si elle existe, bien entendu) ? Lorsqu'il est impossible de donner une formule exacte pour cette valeur, on doit avoir recours à des méthodes ap
From playlist Séminaire Mathematic Park

Irène Waldspurger: "Rank optimality of the Burer-Monteiro factorization"
High Dimensional Hamilton-Jacobi PDEs 2020 Workshop II: PDE and Inverse Problem Methods in Machine Learning "Rank optimality of the Burer-Monteiro factorization" Irène Waldspurger - Université Paris Dauphine Abstract: The Burer-Monteiro factorization is a classical heuristic used to spee
From playlist High Dimensional Hamilton-Jacobi PDEs 2020

Solve a Bernoulli Differential Equation (Part 2)
This video provides an example of how to solve an Bernoulli Differential Equation. The solution is verified graphically. Library: http://mathispower4u.com
From playlist Bernoulli Differential Equations

Periods, cycles, and L-functions: A relative trace formula approach – Wei Zhang – ICM2018
Number Theory Invited Lecture 3.10 Periods, cycles, and L-functions: A relative trace formula approach Wei Zhang Abstract: Motivated by the formulas of Gross–Zagier and Waldspurger, we review conjectures and theorems on automorphic period integrals, special cycles on Shimura varieties, a
From playlist Number Theory