
R - Register Variation with Exploratory Factor Analysis
Lecturer: Dr. Erin M. Buchanan Summer 2019 https://www.patreon.com/statisticsofdoom This video is part of my human language modeling class. On our last video, we will cover exploratory factor analysis to capture the dimensional data that words can present. Note: these videos are part of
From playlist Human Language (ANLY 540)

JASP 0.13.1 Tutorial: Exploratory Factor Analysis (EFA) (Episode 20)
In this JASP tutorial, I go through an Exploratory Factor Analysis (EFA). I use early preliminary data to explore features including Rotation, Factor loadings, Eigenvalues, and how to read the tables in the results. NOTE: This tutorial uses the new preview/beta build of 0.13.1. This build
From playlist JASP Tutorials

This is the other case. The first one was rotation about yb and xa, or if you like x into a and y into b, this one is rotation about xb and ya or x into b and y into a. Now I have a strange feeling that there are again an inifinite number of mixed cases, but I will not think about that now
From playlist Fractal

What is the difference between rotating clockwise and counter clockwise
👉 Learn how to rotate a figure and different points about a fixed point. Most often that point or rotation will be the original but it is important to understand that it does not always have to be at the origin. When rotating it is also important to understand the direction that you will
From playlist Transformations

R - Exploratory Factor Analysis Lecture
Lecturer: Dr. Erin M. Buchanan Fall 2020 https://www.patreon.com/statisticsofdoom This video is part of my structural equation modeling class - you will learn how to perform an exploratory factor analysis as a way to ease into the ideas of SEM. You will learn how to assess the number of
From playlist Structural Equation Modeling 2020

R - Exploratory Factor Analysis Lecture & Example
Lecturer: Dr. Erin M. Buchanan Missouri State University Spring 2016 This video covers basic theory behind exploratory factor analysis and principle components analysis. A complete example of EFA from data screening through parallel analysis, simple structure, fit indices, reliability, a
From playlist Advanced Statistics Videos
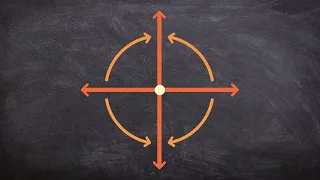
Determining clockwise vs counter clockwise rotations
👉 Learn how to rotate a figure and different points about a fixed point. Most often that point or rotation will be the original but it is important to understand that it does not always have to be at the origin. When rotating it is also important to understand the direction that you will
From playlist Transformations

Derivation of the rotation matrix, the matrix that rotates points in the plane by theta radians counterclockwise. Example of finding the matrix of a linear transformation Check out my Linear Equations playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmD_u31hoZ1D335sSKMvVQ90 Subs
From playlist Linear Equations

Rotations in degrees for counter and clockwise directions
👉 Learn how to rotate a figure and different points about a fixed point. Most often that point or rotation will be the original but it is important to understand that it does not always have to be at the origin. When rotating it is also important to understand the direction that you will
From playlist Transformations

3D Rotations in General: Rodrigues Rotation Formula and Quaternion Exponentials
In this video, we will discover how to rotate any vector through any axis by breaking up a vector into a parallel part and a perpendicular part. Then, we will use vector analysis (cross products and dot products) to derive the Rodrigues rotation formula and finish with a quaternion point o
From playlist Quaternions

Multivariable Calculus | The projection of a vector.
We define the projection of a vector in a certain direction. As an application we decompose a vector into the sum of a parallel and orthogonal component. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Vectors for Multivariable Calculus
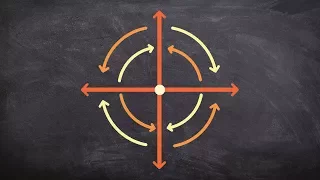
How do the rotations of counter clockwise and clockwise similar
👉 Learn how to rotate a figure and different points about a fixed point. Most often that point or rotation will be the original but it is important to understand that it does not always have to be at the origin. When rotating it is also important to understand the direction that you will
From playlist Transformations

From playlist Unity game engine
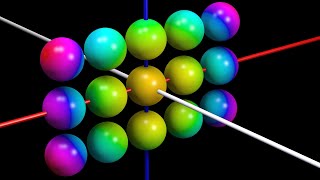
Intuitive Explanation for Intermediate Axis Theorem
Also known as the Dzhanibekov Effect or Tennis Racket Theorem. My Patreon page is at https://www.patreon.com/EugeneK
From playlist Physics

MIT RES.TLL-004 Concept Vignettes View the complete course: http://ocw.mit.edu/RES-TLL-004F13 Instructor: Dan Frey This video leads students through describing the motion of all points on a wobbly disk as a function of time. Properties of time independent rotation matrices are explored.
From playlist MIT STEM Concept Videos

Euler Angles and the Euler Rotation Sequence
In this video we discuss how Euler angles are used to define the relative orientation of one coordinate frame to another. Topics and Timestamps: 0:00 – Introduction and example 2:34 – The Euler Rotation Sequence 16:10 – Matlab animation showing rotation sequence 21:03 – The direction cos
From playlist Flight Mechanics

Lecture 06: 3D Rotations and Complex Representations (CMU 15-462/662)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz2emSh0UQ5iOdT2xRHFHL7E Course information: http://15462.courses.cs.cmu.edu/
From playlist Computer Graphics (CMU 15-462/662)
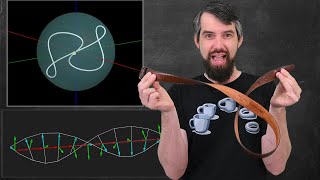
Dirac's Belt Trick: Why a 2π rotation twists space but a 4π rotation fixes it
Visit ► https://brilliant.org/TreforBazett/ to help you learn STEM topics for free, and the first 200 people will get 20% off an annual premium subscription. Check out my MATH MERCH line in collaboration with Beautiful Equations ►https://www.beautifulequation.com/pages/trefor When you t
From playlist Cool Math Series

