
Classify a polynomial then determining if it is a polynomial or not
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?

Is it a polynomial with two variables
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?

Determining if a function is a polynomial or not then determine degree and LC
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?

Determining if a equation is a polynomial or not
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?

The Vandermonde Matrix and Polynomial Interpolation
The Vandermonde matrix is a used in the calculation of interpolating polynomials but is more often encountered in the proof that such polynomial interpolates exist. It is also often encountered in the study of determinants since it has a really nice determinant formula. Chapters 0:00 - In
From playlist Interpolation

A PRG for Gaussian Polynomial Threshold Functions - Daniel Kane
Daniel Kane Harvard University March 15, 2011 We define a polynomial threshold function to be a function of the form f(x) = sgn(p(x)) for p a polynomial. We discuss some recent techniques for dealing with polynomial threshold functions, particular when evaluated on random Gaussians. We sho
From playlist Mathematics

Learn how to identify if a function is a polynomial and identify the degree and LC
👉 Learn how to determine whether a given equation is a polynomial or not. A polynomial function or equation is the sum of one or more terms where each term is either a number, or a number times the independent variable raised to a positive integer exponent. A polynomial equation of functio
From playlist Is it a polynomial or not?
CSDM - Rafael Oliveira - October 12, 2015
http://www.math.ias.edu/calendar/event/83504/1444662900/1444666500
From playlist Computer Science/Discrete Mathematics

19. Saddle Points Continued, Maxmin Principle
MIT 18.065 Matrix Methods in Data Analysis, Signal Processing, and Machine Learning, Spring 2018 Instructor: Gilbert Strang View the complete course: https://ocw.mit.edu/18-065S18 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP63oMNUHXqIUcrkS2PivhN3k Professor Strang c
From playlist MIT 18.065 Matrix Methods in Data Analysis, Signal Processing, and Machine Learning, Spring 2018

The Binomial Chu Vandermonde Identity: a new unification? | Algebraic Calculus Two | Wild Egg Maths
We suggest a novel unification of the Binomial and Chu Vandermonde identities, leading to an unusual introduction of the exponential polyseries, along with Newton's reciprocal polyseries. The main idea is to introduce a generalization of Knuth's rising and falling powers notation, which w
From playlist Algebraic Calculus Two

Linear Algebra 12: Vandermonde determinant (Ch5 Pr2)
How to compute the 3rd Vandermonde determinant. Presented by Peter Brown from the UNSW School of Mathematics and Statistics.
From playlist MATH2501 - Linear Algebra

How to reorder and classify a polynomial based on it's degree and number of terms
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different integer exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials | Equations

👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different interger exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials

Summary for classifying polynomials
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different interger exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials
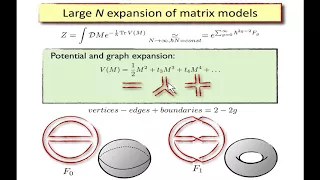
Piotr Sułkowski (6/28/17) Bedlewo: Topological recursion, chord diagrams, and RNA complexes
I will introduce the topological recursion, which is a universal formalism — originating in the realm of matrix models — which assigns an infinite family of symplectic invariants to a given algebraic curve. I will illustrate the power of this formalism by showing how it can be used to solv
From playlist Applied Topology in Będlewo 2017
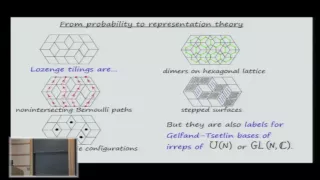
Macdonald processes I - Alexei Borodin
Alexei Borodin Massachussetts Institute of Technology October 8, 2013 Our goal is to explain how certain basic representation theoretic ideas and constructions encapsulated in the form of Macdonald processes lead to nontrivial asymptotic results in various `integrable'; probabilistic probl
From playlist Mathematics

Mapping the Calogero model to anyons by Alexios Polychronakos
PROGRAM: INTEGRABLE SYSTEMS IN MATHEMATICS, CONDENSED MATTER AND STATISTICAL PHYSICS ORGANIZERS: Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE : 16 July 2018 to 10 August 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

Bernd Sturmfels (8/28/18): Learning algebraic varieties from samples
We seek to determine a real algebraic variety from a fixed finite subset of points. Existing methods are studied and new methods are developed. Our focus lies on aspects of topology and algebraic geometry, such as dimension and defining polynomials. All algorithms are tested on a range of
From playlist AATRN 2018

Classifying a polynomial based on its degree and number of terms
👉 Learn how to classify polynomials. A polynomial is an expression of the sums/differences of two or more terms having different integer exponents of the same variable. A polynomial can be classified in two ways: by the number of terms and by its degree. A monomial is an expression of 1
From playlist Classify Polynomials | Equations

Random Matrix Theory and its Applications by Satya Majumdar ( Lecture 3 )
PROGRAM BANGALORE SCHOOL ON STATISTICAL PHYSICS - X ORGANIZERS : Abhishek Dhar and Sanjib Sabhapandit DATE : 17 June 2019 to 28 June 2019 VENUE : Ramanujan Lecture Hall, ICTS Bangalore This advanced level school is the tenth in the series. This is a pedagogical school, aimed at bridgin
From playlist Bangalore School on Statistical Physics - X (2019)