Uniform integrability
In mathematics, uniform integrability is an important concept in real analysis, functional analysis and measure theory, and plays a vital role in the theory of martingales. (Wikipedia).

In mathematics, uniform integrability is an important concept in real analysis, functional analysis and measure theory, and plays a vital role in the theory of martingales. (Wikipedia).


Is many-body localization stable in d greater than 1? by Sumilan Banerjee
PROGRAM: INTEGRABLE SYSTEMS IN MATHEMATICS, CONDENSED MATTER AND STATISTICAL PHYSICS ORGANIZERS: Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE : 16 July 2018 to 10 August 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

The Frustration of being Odd: Universal area law violation in local systems by Fabio Franchini
PROGRAM: INTEGRABLE SYSTEMS IN MATHEMATICS, CONDENSED MATTER AND STATISTICAL PHYSICS ORGANIZERS: Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE : 16 July 2018 to 10 August 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

Some Integrable Models and Supersymmetry by Joseph Samuel
Program : Integrable? ?systems? ?in? ?Mathematics,? ?Condensed? ?Matter? ?and? ?Statistical? ?Physics ORGANIZERS : Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE & TIME : 16 July 2018 to 10 August 2018 VENUE : Ramanujan L
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

Integrability in the Laplacian Growth Problem by Eldad Bettelheim
Program : Integrable systems in Mathematics, Condensed Matter and Statistical Physics ORGANIZERS : Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE & TIME : 16 July 2018 to 10 August 2018 VENUE : Ramanujan L
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

The Unified Transform Method for linear evolution equations (Lecture 3) by David Smith
Program : Integrable systems in Mathematics, Condensed Matter and Statistical Physics ORGANIZERS : Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE & TIME : 16 July 2018 to 10 August 2018 VENUE : Ramanujan L
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

The Unified Transform Method for linear evolution equations (Lecture 2) by David Smith
Program : Integrable systems in Mathematics, Condensed Matter and Statistical Physics ORGANIZERS : Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE & TIME : 16 July 2018 to 10 August 2018 VENUE : Ramanujan L
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

Complex analysis: Locally uniform convergence
This lecture is part of an online undergraduate course on complex analysis. We discuss 3 notions of convergence for functions: pointwise convergence, uniform convergence, and locally uniform convergence, and explain why locally uniform convergence is the best one. As applications we show
From playlist Complex analysis

Calogero Particles and Fluids: A Review (Lecture 2) by Alexios Polychronakos
PROGRAM: INTEGRABLE SYSTEMS IN MATHEMATICS, CONDENSED MATTER AND STATISTICAL PHYSICS ORGANIZERS: Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE : 16 July 2018 to 10 August 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

Dynamical systems and data assimilation by Amit Apte
Program : Integrable systems in Mathematics, Condensed Matter and Statistical Physics ORGANIZERS : Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE & TIME : 16 July 2018 to 10 August 2018 VENUE : Ramanujan L
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

Lecture 24: Uniform Convergence, the Weierstrass M-Test, and Interchanging Limits
MIT 18.100A Real Analysis, Fall 2020 Instructor: Dr. Casey Rodriguez View the complete course: http://ocw.mit.edu/courses/18-100a-real-analysis-fall-2020/ YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP61O7HkcF7UImpM0cR_L2gSw We prove the powerful Weierstrass M-test, a
From playlist MIT 18.100A Real Analysis, Fall 2020

Math 135 Complex Analysis Lecture 13 030515: Poisson Integral Formula; Sequences and Series
Poisson integral formula; quick (?) review of sequences and series: convergence, Cauchy sequence; series (sequence of partial sums), Cauchy criterion; proof of Divergence test; absolute convergence; absolute convergence implies convergence (via Cauchy Criterion); uniform convergence of a s
From playlist Course 8: Complex Analysis

Uniform Solid Cylinder Moment of Inertia Derivation
Deriving the integral equation for the moment of inertia or rotational inertia of a uniform solid cylinder. Want Lecture Notes? http://www.flippingphysics.com/rotational-inertia-solid-cylinder.html This is an AP Physics C: Mechanics topic. Next Video: Parallel Axis Theorem Derivation http
From playlist Rotational Dynamics - AP Physics C: Mechanics

MATH2018 Lecture 4.4 Centre of Mass and Moments of Inertia
In this lecture we show how double integration can be used to understand the dynamics of rotating objects.
From playlist MATH2018 Engineering Mathematics 2D

Real Analysis Ep 34: Uniform convergence of sequences of functions
Episode 34 of my videos for my undergraduate Real Analysis course at Fairfield University. This is a recording of a live class.
From playlist Math 3371 (Real analysis) Fall 2020

Math 131 Spring 2022 041322 Uniform Convergence and Integration
Quick introduction to the Riemann integral. Partition of an interval. Upper and lower sums of a function over a partition. Upper and lower Riemann integrals. Riemann integrable functions. Observations about upper and lower sums; refinements. Common refinement. Lower Riemann integral
From playlist Math 131 Spring 2022 Principles of Mathematical Analysis (Rudin)
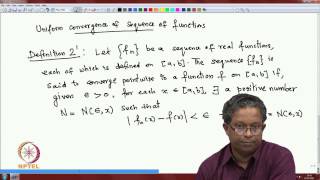
Ordinary Differential Equations and Applications by A. K. Nandakumaran,P. S. Datti & Raju K. George,Department of Mathematics,IISc Bangalore.For more details on NPTEL visit http://nptel.ac.in.
From playlist IISc Bangalore: Ordinary Differential Equations and Applications | CosmoLearning.org Mathematics

Math 131 112116 Uniform Convergence and Integration
Quick introduction to Riemann integrability: partitions, upper and lower sums, upper and lower Riemann integrals, Riemann integrals. Definition: refinement of a partition; common refinement of two partitions. Observation: lower (upper) sums increase (decrease) for a refinement. Theorem:
From playlist Course 7: (Rudin's) Principles of Mathematical Analysis

Uniform Thin Hoop Rotational Inertia Derivation
Deriving the integral equation for the moment of inertia of a rigid body. Also deriving the rotational inertia of a uniform thin hoop. Want Lecture Notes? http://www.flippingphysics.com/rotational-inertia-thin-hoop.html This is an AP Physics C: Mechanics topic. Next Video: Using Integrals
From playlist Rotational Dynamics - AP Physics C: Mechanics

Calogero Particles and Fluids: A Review (Lecture 3) by Alexios Polychronakos
PROGRAM: INTEGRABLE SYSTEMS IN MATHEMATICS, CONDENSED MATTER AND STATISTICAL PHYSICS ORGANIZERS: Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE : 16 July 2018 to 10 August 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics