
Find the Interval of Convergence
How to find the interval of convergence for a power series using the root test.
From playlist Convergence (Calculus)

Interval of Convergence (silent)
Finding the interval of convergence for power series
From playlist 242 spring 2012 exam 3

Calculus: How Convergence Explains The Limit
The limit definition uses the idea of convergence twice (in two slightly different ways). Once the of convergence is grasped, the limit concept becomes easy, even trivial. This clip explains convergence and shows how it can be used to under the limit.
From playlist Summer of Math Exposition Youtube Videos

Newton's Method Interval of Convergence
How to find the Interval of Convergence for Newton-type methods such as Newton's Method, Secant Method, and Finite Difference Method including discussion on Damped Newton's Method and widening the convergence interval. Example code in R hosted on Github: https://github.com/osveliz/numerica
From playlist Root Finding

How To Find The Interval And Radius Of Convergence
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys How To Find The Interval And Radius Of Convergence Given a power series, we find the interval and radius of convergence using the ratio test. In this video all of the steps are shown, including all of the steps for checking the en
From playlist Calculus 2 Exam 4 Playlist

Interval and Radius of Convergence a Power Series using the Ratio Test from Calculus
Interval and Radius of Convergence a Power Series using the Ratio Test from Calculus
From playlist Calculus 2 Exam 4 Playlist

Free ebook http://tinyurl.com/EngMathYT Example on power series and how to find the interval of convergence via the ratio test.
From playlist A second course in university calculus.

Ex 2: Interval of Convergence for Power Series (Centered at 0)
This video provides an example of how to determine the integral of convergence for a power series centered at zero. Site: http://mathispower4u.com
From playlist Power Series

Ch4Pr41d: Interval of Convergence
How to compute the radius of convergence and interval of convergence. This is Chapter 4 Problem 41d from the MATH1231/1241 Calculus notes. Presented by Ms Galina Levitina from UNSW.
From playlist Mathematics 1B (Calculus)
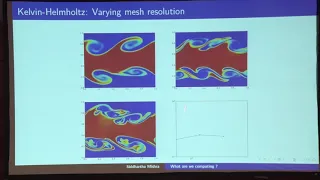
On convergence of numerical schemes for hyperbolic systems of conservation – S. Mishra – ICM2018
Numerical Analysis and Scientific Computing Invited Lecture 15.9 On the convergence of numerical schemes for hyperbolic systems of conservation laws Siddhartha Mishra Abstract: A large variety of efficient numerical methods, of the finite volume, finite difference and DG type, have been
From playlist Numerical Analysis and Scientific Computing

Hyperbolicity and Physical Measures (Lecture 1) by Stefano Luzzatto
PROGRAM SMOOTH AND HOMOGENEOUS DYNAMICS ORGANIZERS: Anish Ghosh, Stefano Luzzatto and Marcelo Viana DATE: 23 September 2019 to 04 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Ergodic theory has its origins in the the work of L. Boltzmann on the kinetic theory of gases.
From playlist Smooth And Homogeneous Dynamics

A. Mondino - Metric measure spaces satisfying Ricci curvature lower bounds 1 (version temporaire)
The idea of compactifying the space of Riemannian manifolds satisfying Ricci curvature lower bounds goes back to Gromov in the '80ies and was pushed by Cheeger-Colding in the ‘90ies, who investigated the structure of spaces arising as Gromov-Hausdorff limits of smooth Riemannian manifolds
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

A. Mondino - Metric measure spaces satisfying Ricci curvature lower bounds 1
The idea of compactifying the space of Riemannian manifolds satisfying Ricci curvature lower bounds goes back to Gromov in the '80ies and was pushed by Cheeger-Colding in the ‘90ies, who investigated the structure of spaces arising as Gromov-Hausdorff limits of smooth Riemannian manifolds
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Mariusz Mirek: Pointwise ergodic theorems for bilinear polynomial averages
We shall discuss the proof of pointwise almost everywhere convergence for the non-conventional (in the sense of Furstenberg and Weiss) bilinear polynomial ergodic averages. This is joint work with Ben Krause and Terry Tao: arXiv:2008.00857. We will also talk about recent progress towards e
From playlist Seminar Series "Harmonic Analysis from the Edge"

Cécile Mailler : Processus de Pólya à valeur mesure
Résumé : Une urne de Pólya est un processus stochastique décrivant la composition d'une urne contenant des boules de différentes couleurs. L'ensemble des couleurs est usuellement un ensemble fini {1, ..., d}. A chaque instant n, une boule est tirée uniformément au hasard dans l'urne (noton
From playlist Probability and Statistics

Lecture 11: The Lebesgue Integral of a Nonnegative Function and Convergence Theorems
MIT 18.102 Introduction to Functional Analysis, Spring 2021 Instructor: Dr. Casey Rodriguez View the complete course: https://ocw.mit.edu/courses/18-102-introduction-to-functional-analysis-spring-2021/ YouTube Playlist: https://www.youtube.com/watch?v=ZWzCHjN3_3s&list=PLUl4u3cNGP63micsJp_
From playlist MIT 18.102 Introduction to Functional Analysis, Spring 2021

G. Alberti - Introduction to minimal surfaces and finite perimeter sets (Part 4)
In these lectures I will first recall the basic notions and results that are needed to study minimal surfaces in the smooth setting (above all the area formula and the first variation of the area), give a short review of the main (classical) techniques for existence results, and then outli
From playlist Ecole d'été 2015 - Théorie géométrique de la mesure et calcul des variations : théorie et applications

What Does It Mean For A Series To Converge?
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys What Does It Mean For A Series To Converge? A series convergences to S if the sequence of partial sums converges to S. In this video I try to explain it and give an example. The example given is a version of Zeno's Dichotomy Paradox
From playlist Calculus 2 Exam 4 Playlist

Alexey Bufetov: Representations of classical Lie groups: two growth regimes
Asymptotic representation theory deals with representations of groups of growing size. For classical Lie groups there are two distinguished regimes of growth. One of them is related to representations of infinite-dimensional groups, and the other appears in combinatorial and probabilistic
From playlist Probability and Statistics
