
Algebra for Beginners | Basics of Algebra
#Algebra is one of the broad parts of mathematics, together with number theory, geometry and analysis. In its most general form, algebra is the study of mathematical symbols and the rules for manipulating these symbols; it is a unifying thread of almost all of mathematics. Table of Conten
From playlist Linear Algebra

Abstract Algebra | Normal Subgroups
We give the definition of a normal subgroup and give some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Algebra is one of the broad areas of mathematics, together with number theory, geometry and analysis. In its most general form, #algebra is the study of mathematical symbols and the rules for manipulating these symbols; it is a unifying thread of almost all of mathematics. In this course
From playlist Algebra
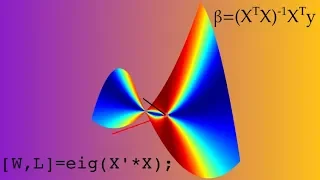
This is part of an online course on beginner/intermediate linear algebra, which presents theory and implementation in MATLAB and Python. The course is designed for people interested in applying linear algebra to applications in multivariate signal processing, statistics, and data science.
From playlist Linear algebra: theory and implementation

Group Definition (expanded) - Abstract Algebra
The group is the most fundamental object you will study in abstract algebra. Groups generalize a wide variety of mathematical sets: the integers, symmetries of shapes, modular arithmetic, NxM matrices, and much more. After learning about groups in detail, you will then be ready to contin
From playlist Abstract Algebra

13C Norm and Distance in Euclidean n Space
Norm and distance in Euclidean n-Space.
From playlist Linear Algebra

Bruno de Mendonca Braga: Coarse equivalences of metric spaces and out automorphisms of Roe algebras
Talk by Bruno Braga in Global Noncommutative Geometry Seminar (Americas) http://www.math.wustl.edu/~xtang/NCG-Seminar.html on September 2, 2020.
From playlist Global Noncommutative Geometry Seminar (Americas)
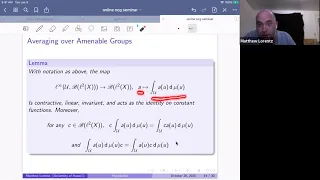
Matthew Lorentz: The Hochschild cohomology of uniform Roe algebras
Talk by Jonathan Rosenberg in Global Noncommutative Geometry Seminar (Americas) http://www.math.wustl.edu/~xtang/NCG-Seminar.html on October 28, 2020.
From playlist Global Noncommutative Geometry Seminar (Americas)

Complex dynamics and arithmetic equidistribution – Laura DeMarco – ICM2018
Dynamical Systems and Ordinary Differential Equations Invited Lecture 9.5 Complex dynamics and arithmetic equidistribution Laura DeMarco Abstract: I will explain a notion of arithmetic equidistribution that has found application in the study of complex dynamical systems. It was first int
From playlist Dynamical Systems and ODE
Kristin Courtney: C*-structure on images of completely positive order zero maps
Talk by Kristin Courtney in Global Noncommutative Geometry Seminar (Americas) http://www.math.wustl.edu/~xtang/NCG-Seminar.html on September 16, 2020.
From playlist Global Noncommutative Geometry Seminar (Americas)

Valentin Suder - Sparse Permutations with Low Differential Uniformity
Sparse Permutations with Low Differential Uniformity
From playlist Journées Codage et Cryptographie 2014

Perfectoid spaces (Lecture 3) by Kiran Kedlaya
PERFECTOID SPACES ORGANIZERS: Debargha Banerjee, Denis Benois, Chitrabhanu Chaudhuri, and Narasimha Kumar Cheraku DATE & TIME: 09 September 2019 to 20 September 2019 VENUE: Madhava Lecture Hall, ICTS, Bangalore Scientific committee: Jacques Tilouine (University of Paris, France) Eknath
From playlist Perfectoid Spaces 2019

Antonio Rieser (03/29/23) Algebraic Topology for Graphs & Mesoscopic Spaces: Homotopy & Sheaf Theory
Title: Algebraic Topology for Graphs and Mesoscopic Spaces: Homotopy and Sheaf Theory Abstract: In this talk, we introduce the notion of a mesoscopic space: a metric space decorated with a privileged scale, and we survey recent developments in the algebraic topology of such spaces. Our ap
From playlist AATRN 2023

The orbit method for (certain) pro-p groups (Lecture - 03) by Uri Onn
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation
The hyperbolic Ax-Lindemann conjecture - Emmanuel Ullmo
Emmanuel Ullmo Université Paris-Sud February 7, 2014 The hyperbolic Ax Lindemann conjecture is a functional transcendental statement which describes the closure of "algebraic flows" on Shimura varieties. We will describe the proof of this conjecture and its consequences for the André-Oort
From playlist Mathematics

Advanced Linear Algebra Full Video Course
Linear algebra is central to almost all areas of mathematics. For instance, #linearalgebra is fundamental in modern presentations of geometry, including for defining basic objects such as lines, planes and rotations. Also, functional analysis may be basically viewed as the application of
From playlist Linear Algebra

Uniformly valuative stability of polarized varieties and applications
Speaker: Yaxiong Liu (Tsinghua University) Abstract: In the study of K-stability, Fujita and Li proposed the valuative criterion of K-stability on Fano varieties, which has played an essential role of the algebraic theory of K-stability. Recently, Dervan-Legendre considered the valuative
From playlist Informal Geometric Analysis Seminar

Math 060 Linear Algebra 31 112614: Normal Matrices
Normal matrices: characterization of unitarily diagonalizable matrices.
From playlist Course 4: Linear Algebra

