
Here I prove the Heine-Borel Theorem, one of the most fundamental theorems in analysis. It says that in R^n, all boxes must be compact. The proof itself is very neat, and uses a bisection-type argument. Enjoy! Topology Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmA13vj9xkHG
From playlist Topology

Calculus 5.3 The Fundamental Theorem of Calculus
My notes are available at http://asherbroberts.com/ (so you can write along with me). Calculus: Early Transcendentals 8th Edition by James Stewart
From playlist Calculus

Theory of numbers: Fermat's theorem
This lecture is part of an online undergraduate course on the theory of numbers. We prove Fermat's theorem a^p = a mod p. We then define the order of a number mod p and use Fermat's theorem to show the order of a divides p-1. We apply this to testing some Fermat and Mersenne numbers to se
From playlist Theory of numbers

Number Theory | A very special case of Fermat's Last Theorem
We prove a very simple case of Fermat's Last Theorem. Interestingly, this case is fairly easy to prove which highlights the allure of the theorem as a whole -- especially given the fact that much of modern number theory was developed as part of the program that ended in the full proof. ht
From playlist Number Theory
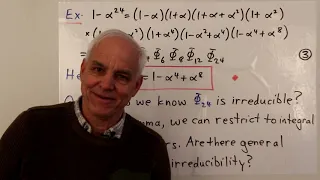
Irreducibility and the Schoenemann-Eisenstein criterion | Famous Math Probs 20b | N J Wildberger
In the context of defining and computing the cyclotomic polynumbers (or polynomials), we consider irreducibility. Gauss's lemma connects irreducibility over the integers to irreducibility over the rational numbers. Then we describe T. Schoenemann's irreducibility criterion, which uses some
From playlist Famous Math Problems

Theory of numbers: Congruences: Euler's theorem
This lecture is part of an online undergraduate course on the theory of numbers. We prove Euler's theorem, a generalization of Fermat's theorem to non-prime moduli, by using Lagrange's theorem and group theory. As an application of Fermat's theorem we show there are infinitely many prim
From playlist Theory of numbers

Introduction to additive combinatorics lecture 1.8 --- Plünnecke's theorem
In this video I present a proof of Plünnecke's theorem due to George Petridis, which also uses some arguments of Imre Ruzsa. Plünnecke's theorem is a very useful tool in additive combinatorics, which implies that if A is a set of integers such that |A+A| is at most C|A|, then for any pair
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

Can you prove it? The Extreme Value Theorem
Extreme Value Theorem Proof In this video, I prove one of the most fundamental results of calculus and analysis, namely that a continuous function on [a,b] must attain a maximum and a minimum. Do you know how to prove it? Watch this video and find out! Bolzano-Weierstrass Theorem: https:
From playlist Real Analysis

Fermat's Little Theorem ← Number Theory
Fermat's Little Theorem was observed by Fermat and proven by Euler, who generalized the theorem significantly. This theorem aids in dividing extremely large numbers and can aid in testing numbers to see if they are prime. For more advanced students, this theorem can be easily proven usin
From playlist Number Theory

Calculus 1 (Stewart) Ep 22, Mean Value Theorem (Oct 28, 2021)
This is a recording of a live class for Math 1171, Calculus 1, an undergraduate course for math majors (and others) at Fairfield University, Fall 2021. The textbook is Stewart. PDF of the written notes, and a list of all episodes is at the class website. Class website: http://cstaecker.f
From playlist Math 1171 (Calculus 1) Fall 2021

Equidistribution of Unipotent Random Walks on Homogeneous spaces by Emmanuel Breuillard
PROGRAM : ERGODIC THEORY AND DYNAMICAL SYSTEMS (HYBRID) ORGANIZERS : C. S. Aravinda (TIFR-CAM, Bengaluru), Anish Ghosh (TIFR, Mumbai) and Riddhi Shah (JNU, New Delhi) DATE : 05 December 2022 to 16 December 2022 VENUE : Ramanujan Lecture Hall and Online The programme will have an emphasis
From playlist Ergodic Theory and Dynamical Systems 2022

What is Green's theorem? Chris Tisdell UNSW
This lecture discusses Green's theorem in the plane. Green's theorem not only gives a relationship between double integrals and line integrals, but it also gives a relationship between "curl" and "circulation". In addition, Gauss' divergence theorem in the plane is also discussed, whic
From playlist Vector Calculus @ UNSW Sydney. Dr Chris Tisdell

Real Analysis Ep 32: The Mean Value Theorem
Episode 32 of my videos for my undergraduate Real Analysis course at Fairfield University. This is a recording of a live class. This episode is more about the mean value theorem and related ideas. Class webpage: http://cstaecker.fairfield.edu/~cstaecker/courses/2020f3371/ Chris Staecker
From playlist Math 3371 (Real analysis) Fall 2020

Pythagorean theorem - What is it?
► My Geometry course: https://www.kristakingmath.com/geometry-course Pythagorean theorem is super important in math. You will probably learn about it for the first time in Algebra, but you will literally use it in Algebra, Geometry, Trigonometry, Precalculus, Calculus, and beyond! That’s
From playlist Geometry

Wolfram Physics Project: Working Session Sept. 15, 2020 [Physicalization of Metamathematics]
This is a Wolfram Physics Project working session on metamathematics and its physicalization in the Wolfram Model. Begins at 10:15 Originally livestreamed at: https://twitch.tv/stephen_wolfram Stay up-to-date on this project by visiting our website: http://wolfr.am/physics Check out the
From playlist Wolfram Physics Project Livestream Archive

Johnathan Bush (7/8/2020): Borsuk–Ulam theorems for maps into higher-dimensional codomains
Title: Borsuk–Ulam theorems for maps into higher-dimensional codomains Abstract: I will describe Borsuk-Ulam theorems for maps of spheres into higher-dimensional codomains. Given a continuous map from a sphere to Euclidean space, we say the map is odd if it respects the standard antipodal
From playlist AATRN 2020

Worldwide Calculus: Extrema and the Mean Value Theorem
Lecture on 'Extrema and the Mean Value Theorem' from 'Worldwide Differential Calculus' and 'Worldwide AP Calculus'. For more lecture videos and $10 digital textbooks, visit www.centerofmath.org.
From playlist Worldwide Single-Variable Calculus for AP®

Stokes' Theorem and Green's Theorem
Stokes' theorem is an extremely powerful result in mathematical physics. It allows us to quantify how much a vector field is circulating or rotating, based on the integral of the curl. @eigensteve on Twitter eigensteve.com databookuw.com %%% CHAPTERS %%% 0:00 Stoke's Theorem Overview
From playlist Engineering Math: Vector Calculus and Partial Differential Equations

Green's Theorem. Chris Tisdell UNSW
This is the 2nd lecture on Green's theorem and its use. In this lecture we explore some interesting applications of Green's theorem and present several examples. Also some proofs are discussed.
From playlist Vector Calculus @ UNSW Sydney. Dr Chris Tisdell

Multidimensional Bolzano Weierstraß
In this video, I prove the celebrated Bolzano-Weierstraß theorem in n dimensions, which says that a bounded sequence in R^n must have a convergent subsequence. This is the most important fact in analysis, and a lot of nice results follow from it Bolzano-Weierstraß: https://youtu.be/PapmU
From playlist Topology