
Irrigation Efficiencies - Part 1
From playlist TEMP 1

The idea of ‘atonement’ sounds very old-fashioned and is deeply rooted in religious tradition. To atone means, in essence, to acknowledge one’s capacity for wrongness and one’s readiness for apology and desire for change. It’s a concept that every society needs at its center. For gifts and
From playlist RELATIONSHIPS

Is There an Alternative to Political Correctness?
Political correctness aims for some very nice results, but its means have a habit of upsetting a lot of people. Might there be an alternative to it? We think there is, and it’s called Politeness. If you like our films, take a look at our shop (we ship worldwide): https://goo.gl/iVqWJ1 Joi
From playlist WORK + CAPITALISM

Proof: Supremum and Infimum are Unique | Real Analysis
If a subset of the real numbers has a supremum or infimum, then they are unique! Uniqueness is a tremendously important property, so although it is almost complete trivial as far as difficulty goes in this case, we would be ill-advised to not prove these properties! In this lesson we'll be
From playlist Real Analysis
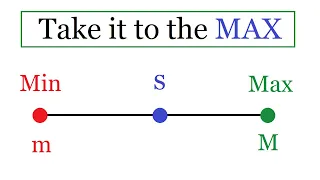
Maximum and Minimum of a set In this video, I define the maximum and minimum of a set, and show that they don't always exist. Enjoy! Check out my Real Numbers Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmCZggpJZvUXnUzaw7fHCtoh
From playlist Real Numbers
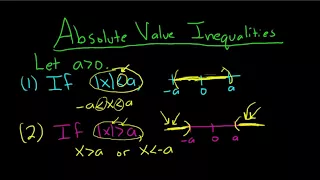
How to Solve Absolute Value Inequalities
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys How to Solve Absolute Value Inequalities
From playlist College Algebra

Absolute Value Equations & Inequalities (1 of 4: Visualising an equation)
More resources available at www.misterwootube.com
From playlist Working with Functions

Math 101 Fall 2017 112917 Introduction to Compact Sets
Definition of an open cover. Definition of a compact set (in the real numbers). Examples and non-examples. Properties of compact sets: compact sets are bounded. Compact sets are closed. Closed subsets of compact sets are compact. Infinite subsets of compact sets have accumulation poi
From playlist Course 6: Introduction to Analysis (Fall 2017)

What is the definition of absolute value
http://www.freemathvideos.com In this video playlist you will learn how to solve and graph absolute value equations and inequalities. When working with absolute value equations and functions it is important to understand that the absolute value symbol represents the absolute distance from
From playlist Solve Absolute Value Equations

Lecture 20 - Introduction to NP-completeness
This is Lecture 20 of the CSE373 (Analysis of Algorithms) taught by Professor Steven Skiena [http://www.cs.sunysb.edu/~skiena/] at Stony Brook University in 1997. The lecture slides are available at: http://www.cs.sunysb.edu/~algorith/video-lectures/1997/lecture22.pdf
From playlist CSE373 - Analysis of Algorithms - 1997 SBU

CSE 373 --- Lecture 20: Satisfiability (Fall 2021)
11/23/21
From playlist CSE373 --- Analysis of Algorithms (Fall 2021)

On Approximability of CSPs on Satisfiable Instances - Subhash Khot
Computer Science/Discrete Mathematics Seminar I Topic: On Approximability of CSPs on Satisfiable Instances Speaker: Subhash Khot Affiliation: New York University Date: November 22, 2021 Constraint Satisfaction Problems (CSPs) are among the most well-studied problems in Computer Science,
From playlist Mathematics

This is Lecture 21 of the CSE373 (Analysis of Algorithms) taught by Professor Steven Skiena [http://www.cs.sunysb.edu/~skiena/] at Stony Brook University in 1997. The lecture slides are available at: http://www.cs.sunysb.edu/~algorith/video-lectures/1997/lecture23.pdf
From playlist CSE373 - Analysis of Algorithms - 1997 SBU

CSE 373 -- Lecture 24, Fall 2020
From playlist CSE 373 -- Fall 2020

This is Lecture 24 of the CSE373 (Analysis of Algorithms) course taught by Professor Steven Skiena [http://www3.cs.stonybrook.edu/~skiena/] at Stony Brook University in 2016. The lecture slides are available at: https://www.cs.stonybrook.edu/~skiena/373/newlectures/lecture20.pdf More inf
From playlist CSE373 - Analysis of Algorithms 2016 SBU
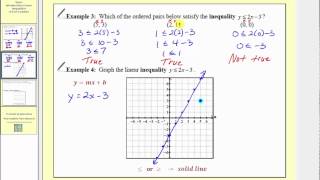
Introduction to Linear Inequalities in Two Variables (L11.6)
This lesson introduces linear inequalities in two variables. Video content created by Jenifer Bohart, William Meacham, Judy Sutor, and Donna Guhse from SCC (CC-BY 4.0)
From playlist Solving Linear Inequalities in Two Variables

Yongnam Lee: Q-Gorenstein Deformations and their applications
In this talk we will discuss Q-Gorenstein schemes and Q-Gorenstein morphisms in a general setting. Based on the notion of Q-Gorenstein morphism, we define the notion of Q-Gorenstein deformations and discuss their properties. Versal properties of Q-Gorenstein deformations and their applicat
From playlist HIM Lectures: Junior Trimester Program "Algebraic Geometry"

Hall's Theorem and Condition for Bipartite Matchings | Graph Theory, Hall's Marriage Theorem
What are Hall's Theorem and Hall's Condition for bipartite matchings in graph theory? Also sometimes called Hall's marriage theorem, we'll be going it in today's video graph theory lesson! A bipartite graph with partite sets U and W, where U has as many or fewer vertices than W, satisfie
From playlist Graph Theory

CERIAS Security: An Algebra for Specifying High-level Security Policies 2/5
Clip 2/5 Speaker: Qihua Wang · Purdue University A high-level security policy states an overall requirement for a sensitive task. One example of a high-level security policy is a separation of duty policy, which requires a sensitive task to be performed by a team of at least k users.
From playlist The CERIAS Security Seminars 2006

Observability is a hot tech topic yet has also become one of the industry’s most overused buzzwords. The term means understanding the behavior, performance, and other aspects of cloud infrastructure and cloud apps based on the data they generate, such as metrics, events, logs and traces. O
From playlist Software Development