
LieGroups and Lie Algebras: Lesson 4 - The Classical Groups Part II
Lie Groups and Lie Algebras: Lesson 4 - The Classical Groups Part II We introduce the idea of the classical matrix groups and their associated carrier spaces. In this video we discuss the representation of complex numbers and quaternions as matrices and then we discuss the idea of a metri
From playlist Lie Groups and Lie Algebras

Lie Groups and Lie Algebras: Lesson 13 - Continuous Groups defined
Lie Groups and Lie Algebras: Lesson 13 - Continuous Groups defined In this lecture we define a "continuous groups" and show the connection between the algebraic properties of a group with topological properties. Please consider supporting this channel via Patreon: https://www.patreon.co
From playlist Lie Groups and Lie Algebras
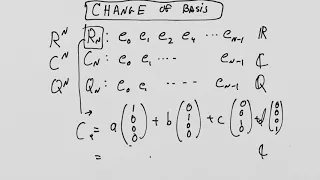
Lie Groups and Lie Algebras: Lesson 3 - Classical Groups Part I
Lie Groups and Lie Algebras: Lesson 3 - Classical Groups Part I We introduce the idea of the classical matrix groups and their associated carrier spaces. Please consider supporting this channel via Patreon: https://www.patreon.com/XYLYXYLYX
From playlist Lie Groups and Lie Algebras
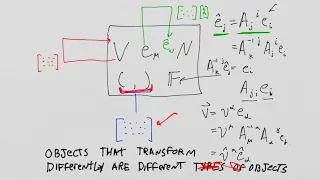
Lie Groups and Lie Algebras: Lesson 7 - The Classical Groups Part V
Lie Groups and Lie Algebras: Lesson 7 - The Classical Groups Part V We discuss the matrix interpretation of the metric even more, since it is critical to our understanding of the classical groups. Please consider supporting this channel via Patreon: https://www.patreon.com/XYLYXYLYX
From playlist Lie Groups and Lie Algebras

Lie Groups and Lie Algebras: Lesson 12 - The Classical Groups Part X (redux)
Lie Groups and Lie Algebras: Lesson 12 - The Classical Groups Part X (redux) We name the classical groups, finally! This video ended a bit short, I added the missing part in the "redux" version of this lesson. Please consider supporting this channel via Patreon: https://www.patreon.com/
From playlist Lie Groups and Lie Algebras

Introduction to Classical Physics
Physics is the grandaddy of the sciences! When those ancient dudes in togas were philosophizing about the way the universe works, they were setting the stage for what we now know of as physics, even though it didn't really get going until Galileo and Newton. Why should we study physics? Wh
From playlist Classical Physics

This lecture is part of an online graduate course on Lie groups. We give an introductory survey of Lie groups theory by describing some examples of Lie groups in low dimensions. Some recommended books: Lie algebras and Lie groups by Serre (anything by Serre is well worth reading) Repre
From playlist Lie groups

Lia Groups and Lie Algebras Lesson 6 (redux):The classical groups part IV
Lia Groups and Lie Algebras Lesson 6 (redux):The classical groups part IV
From playlist Lie Groups and Lie Algebras

A group is (in a sense) the simplest structure in which we can do the familiar tasks associated with "algebra." First, in this video, we review the definition of a group.
From playlist Modern Algebra - Chapter 15 (groups)
Tony Feng - 1/3 Derived Aspects of the Langlands Program
We discuss ways in which derived structures have recently emerged in connection with the Langlands correspondence, with an emphasis on derived Galois deformation rings and derived Hecke algebras. Michael Harris (Columbia Univ.) Tony Feng (MIT)
From playlist 2022 Summer School on the Langlands program

Classical and Digital Topological Groups
A research talk presented at the Fairfield University Mathematics Research Seminar, October 6, 2022. Should be accessible to a general mathematics audience, combining ideas from topology, graph theory, and abstract algebra. The paper is by me and Dae Woong Lee, available here: https://arx
From playlist Research & conference talks

Yonatan Harpaz - New perspectives in hermitian K-theory III
For questions and discussions of the lecture please go to our discussion forum: https://www.uni-muenster.de/TopologyQA/index.php?qa=k%26l-conference This lecture is part of the event "New perspectives on K- and L-theory", 21-25 September 2020, hosted by Mathematics Münster: https://go.wwu
From playlist New perspectives on K- and L-theory

Ernst-Ulrich Gekeler: Algebraic curves with many rational points over non-prime finite fields
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist SPECIAL 7th European congress of Mathematics Berlin 2016.

Ernesto Lupercio: On the moduli space for Quantum Toric Varieties
Talk by Ernesto Lupercio in Global Noncommutative Geometry Seminar (Americas) on November 5, 2021, https://globalncgseminar.org/talks/tba-17/
From playlist Global Noncommutative Geometry Seminar (Americas)

Hodge theory and algebraic cycles - Phillip Griffiths
Geometry and Arithmetic: 61st Birthday of Pierre Deligne Phillip Griffiths Institute for Advanced Study October 18, 2005 Pierre Deligne, Professor Emeritus, School of Mathematics. On the occasion of the sixty-first birthday of Pierre Deligne, the School of Mathematics will be hosting a f
From playlist Pierre Deligne 61st Birthday

Marko Tadic - Unitarizability in generalised rank three case for classical p-adic groups
J. Arthur has classified irreducible tempered representations of classical p-adic groups. C. Moeglin has singled out parameters of cuspidal representations among them. Further, she gave a simple formula forcuspidal reducibilities (in the generalised rank one). In our talk, we sh
From playlist Reductive groups and automorphic forms. Dedicated to the French school of automorphic forms and in memory of Roger Godement.

Yonatan Harpaz - New perspectives in hermitian K-theory I
For questions and discussions of the lecture please go to our discussion forum: https://www.uni-muenster.de/TopologyQA/index.php?qa=k%26l-conference This lecture is part of the event "New perspectives on K- and L-theory", 21-25 September 2020, hosted by Mathematics Münster: https://go.wwu
From playlist New perspectives on K- and L-theory

A Satake Isomorphism Mod.p - Guy Henniart
A Satake Isomorphism Mod.p Guy Henniart November 4, 2010 Let F be a locally compact non-Archimedean field, p its residue characteristic and G a connected reductive algebraic group over F . The classical Satake isomorphism describes the Hecke algebra (over the field of complex numbers) of
From playlist Mathematics

Symmetric Groups (Abstract Algebra)
Symmetric groups are some of the most essential types of finite groups. A symmetric group is the group of permutations on a set. The group of permutations on a set of n-elements is denoted S_n. Symmetric groups capture the history of abstract algebra, provide a wide range of examples in
From playlist Abstract Algebra

Why was Connes' embedding conjecture refuted and there are still no known... -Michael Chapman
Stability and Testability Topic: Why was Connes' embedding conjecture refuted and there are still no known non-hyperlinear groups? Speaker: Michael Chapman Affiliation: Hebrew University Date: March 24, 2021 For more video please visit http://video.ias.edu
From playlist Stability and Testability