
Prealgebra 4.3a - Complex Fractions
Complex Fractions. What they are, and one technique for simplifying them.
From playlist Prealgebra Chapter 4 (Complete chapter)

Prealgebra Lecture 4.3: How to Multiply and Divide Fractions
https://www.patreon.com/ProfessorLeonard Prealgebra Lecture 4.3: Multiplying and Dividing Fractions
From playlist Prealgebra (Full Length Videos)

How to subtract two large polynomials by rewriting as an addition problem
👉 Learn how to subtract polynomials. To subtract polynomials, we first simplify the polynomials by removing all brackets. Then, we combine like terms. Like terms are terms that share the same base and power for each variable. When you have identified the like terms, we then apply the requ
From playlist How to subtract polynomials

👉 Learn how to subtract polynomials. To subtract polynomials, we first simplify the polynomials by removing all brackets. Then, we combine like terms. Like terms are terms that share the same base and power for each variable. When you have identified the like terms, we then apply the requ
From playlist How to subtract polynomials

How to subtract two trinomials polynomials
👉 Learn how to subtract polynomials. To subtract polynomials, we first simplify the polynomials by removing all brackets. Then, we combine like terms. Like terms are terms that share the same base and power for each variable. When you have identified the like terms, we then apply the requ
From playlist How to subtract polynomials
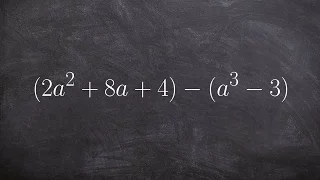
How to simplify the subtraction of two polynomials
👉 Learn how to subtract polynomials. To subtract polynomials, we first simplify the polynomials by removing all brackets. Then, we combine like terms. Like terms are terms that share the same base and power for each variable. When you have identified the like terms, we then apply the requ
From playlist How to subtract polynomials

Simplify a Complex Fraction and label restrictions
👉 Learn how to simplify complex fractions. To simplify complex fractions having the addition/subtraction of more than one fractions in the numerator or/and in the denominator we first evaluate the numerator or/and the denominator separately to have one fraction in the numerator and in the
From playlist How to Simplify Complex Fractions with Binomials

👉 Learn how to subtract polynomials. To subtract polynomials, we first simplify the polynomials by removing all brackets. Then, we combine like terms. Like terms are terms that share the same base and power for each variable. When you have identified the like terms, we then apply the requ
From playlist How to subtract polynomials

👉 Learn how to subtract polynomials. To subtract polynomials, we first simplify the polynomials by removing all brackets. Then, we combine like terms. Like terms are terms that share the same base and power for each variable. When you have identified the like terms, we then apply the requ
From playlist How to subtract polynomials

Winter School JTP: Introduction to Fukaya categories, James Pascaleff, Lecture 1
This minicourse will provide an introduction to Fukaya categories. I will assume that participants are also attending Keller’s course on A∞ categories. Lecture 1: Basics of symplectic geometry for Fukaya categories. Symplectic manifolds; Lagrangian submanifolds; exactness conditions;
From playlist Winter School on “Connections between representation Winter School on “Connections between representation theory and geometry"

Mean curvature flow in high co-dimension - William Minicozzi
Analysis Seminar Topic: Mean curvature flow in high co-dimension Speaker: William Minicozzi Affiliation: Massachusetts Institute of Technology Date: April 26, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

C0 contact geometry of isotropic submanifolds - Maksim Stokić
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Three 20-minute research talks Topic: C0 contact geometry of isotropic submanifolds Speaker: Maksim Stokić Affiliation: Tel Aviv University Date: May 27, 2022 Homeomorphism is called contact if it can be written a
From playlist Mathematics

Manifolds - Part 14 - Submanifolds
Support the channel on Steady: https://steadyhq.com/en/brightsideofmaths Or support me via PayPal: https://paypal.me/brightmaths Or via Ko-fi: https://ko-fi.com/thebrightsideofmathematics Or via Patreon: https://www.patreon.com/bsom Or via other methods: https://thebrightsideofmathematics.
From playlist Manifolds

Producing Minimal Submanifolds via Gauge Theory
Daniel Stern (U Chicago) Abstract: The self-dual U(1)-Yang-Mills-Higgs functionals are a natural family of energies associated to sections and metric connections of Hermitian line bundles, whose critical points (particularly in the 2-dimensional and Kaehler settings) are objects of long-st
From playlist Informal Geometric Analysis Seminar

Jake Solomon: The degenerate special Lagrangian equation
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Jean-Morlet Chair - Lalonde/Teleman

Sachchidanand Prasad: Morse-Bott Flows and Cut Locus of Submanifolds
Sachchidanand Prasad, Indian Institute of Science Education and Research Kolkata Title: Morse-Bott Flows and Cut Locus of Submanifolds We will recall the notion of cut locus of closed submanifolds in a complete Riemannian manifold. Using Morse-Bott flows, it can be seen that the complement
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022

Paola Frediani: Totally geodesic submanifolds in the Torelli locus
We will describe recent results on totally geodesic submanifolds and Shimura subvarieties of Ag contained in the Torelli locus Tg. Using the second fundamental form of the Torelli map we give an upper bound on the dimension of totally geodesic submanifolds contained in Tg, which depends on
From playlist HIM Lectures: Junior Trimester Program "Algebraic Geometry"

François Lalonde - Applications of Quantum homology to Symplectic Topology (Part 3)
The first two lectures will present the fundamental results of symplectic topology : basic definitions, Moser’s lemma, normal forms of the symplectic structure near symplectic and Lagrangian submanifolds, characterization of Hamiltonian fibrations over any CW-complex. The third course will
From playlist École d’été 2012 - Feuilletages, Courbes pseudoholomorphes, Applications
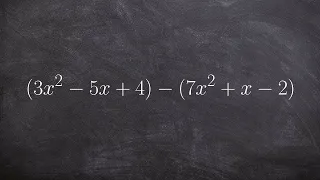
Overview subtracting polynomials teacher explains how to
👉 Learn how to subtract polynomials. To subtract polynomials, we first simplify the polynomials by removing all brackets. Then, we combine like terms. Like terms are terms that share the same base and power for each variable. When you have identified the like terms, we then apply the requ
From playlist How to subtract polynomials

François Lalonde - Applications of Quantum homology to Symplectic Topology (Part 4)
The first two lectures will present the fundamental results of symplectic topology : basic definitions, Moser’s lemma, normal forms of the symplectic structure near symplectic and Lagrangian submanifolds, characterization of Hamiltonian fibrations over any CW-complex. The third course will
From playlist École d’été 2012 - Feuilletages, Courbes pseudoholomorphes, Applications