
Exploring Symplectic Embeddings and Symplectic Capacities
Speakers o Alex Gajewski o Eli Goldin o Jakwanul Safin o Junhui Zhang Project Leader: Kyler Siegel Abstract: Given a domain (e.g. a ball) in Euclidean space, we can ask what is its volume. We can also ask when one domain can be embedded into another one without distorting volumes. These
From playlist 2019 Summer REU Presentations

Symplectic topology and the loop space - Jingyu Zhao
Topic: Symplectic topology and the loop space Speaker: Jingyu Zhao, Member, School of Mathematics Time/Room: 4:45pm - 5:00pm/S-101 More videos on http://video.ias.edu
From playlist Mathematics

What exactly is space? Brian Greene explains what the "stuff" around us is. Subscribe to our YouTube Channel for all the latest from World Science U. Visit our Website: http://www.worldscienceu.com/ Like us on Facebook: https://www.facebook.com/worldscienceu Follow us on Twitter: https:
From playlist Science Unplugged: Physics

Is there any place in the Universe where there's truly nothing? Consider the gaps between stars and galaxies? Or the gaps between atoms? What are the properties of nothing?
From playlist Guide to Space

Symplectic Inverse Spectral Theory in the Regime for Toric Systems . . . and Beyond - San Vu Ngoc
San Vu Ngoc University of Rennes, France January 27, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics
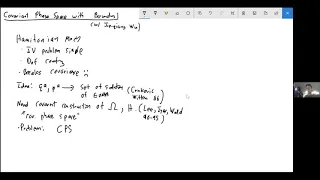
Covariant Phase Space with Boundaries - Daniel Harlow
More videos on http://video.ias.edu
From playlist Natural Sciences

From playlist Unlisted LA Videos

Symmetries show up everywhere in physics. But what is a symmetry? While the symmetries of shapes can be interesting, a lot of times, we are more interested in symmetries of space or symmetries of spacetime. To describe these, we need to build "invariants" which give a mathematical represen
From playlist Relativity

Symplectic fillings and star surgery - Laura Starkston
Laura Starkston University of Texas, Austin September 25, 2014 Although the existence of a symplectic filling is well-understood for many contact 3-manifolds, complete classifications of all symplectic fillings of a particular contact manifold are more rare. Relying on a recognition theor
From playlist Mathematics

Brent Pym: Holomorphic Poisson structures - lecture 3
The notion of a Poisson manifold originated in mathematical physics, where it is used to describe the equations of motion of classical mechanical systems, but it is nowadays connected with many different parts of mathematics. A key feature of any Poisson manifold is that it carries a cano
From playlist Virtual Conference

Stability conditions in symplectic topology – Ivan Smith – ICM2018
Geometry Invited Lecture 5.8 Stability conditions in symplectic topology Ivan Smith Abstract: We discuss potential (largely speculative) applications of Bridgeland’s theory of stability conditions to symplectic mapping class groups. ICM 2018 – International Congress of Mathematicians
From playlist Geometry

A tale of two conjectures: from Mahler to Viterbo - Yaron Ostrover
Members' Seminar Topic: A tale of two conjectures: from Mahler to Viterbo. Speaker: Yaron Ostrover Affiliation: Tel Aviv University, von Neumann Fellow, School of Mathematics Date: November 19, 2018 For more video please visit http://video.ias.edu
From playlist Mathematics

Act globally, compute...points and localization - Tara Holm
Tara Holm Cornell University; von Neumann Fellow, School of Mathematics October 20, 2014 Localization is a topological technique that allows us to make global equivariant computations in terms of local data at the fixed points. For example, we may compute a global integral by summing inte
From playlist Mathematics

Lectures on Homological Mirror Symmetry II - Sheridan Nick
Lectures on Homological Mirror Symmetry Sheridan Nick Institute for Advanced Study; Member, School of Mathematics November 4, 2013
From playlist Mathematics
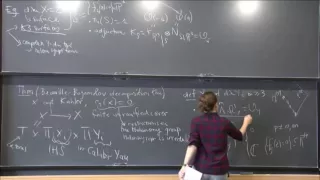
Symplectic forms in algebraic geometry - Giulia Saccà
Giulia Saccà Member, School of Mathematics January 30, 2015 Imposing the existence of a holomorphic symplectic form on a projective algebraic variety is a very strong condition. After describing various instances of this phenomenon (among which is the fact that so few examples are known!)
From playlist Mathematics

Rigidity and recurrence in symplectic dynamics - Matthias Schwarz
Members’ Seminar Topic: Rigidity and recurrence in symplectic dynamics Speaker: Matthias Schwarz, Universität Leipzig; Member, School of Mathematics Date: December 11, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Brent Pym: Holomorphic Poisson structures - lecture 2
The notion of a Poisson manifold originated in mathematical physics, where it is used to describe the equations of motion of classical mechanical systems, but it is nowadays connected with many different parts of mathematics. A key feature of any Poisson manifold is that it carries a cano
From playlist Virtual Conference

Pavel Etingof - "D-modules on Poisson varieties and Poisson traces"
Pavel Etingof delivers a research talk on "D-modules on Poisson varieties and Poisson traces" at the Worldwide Center of Mathematics
From playlist Center of Math Research: the Worldwide Lecture Seminar Series

Constructions in symplectic and contact topology via h-principles - Oleg Lazarev
More videos on http://video.ias.edu
From playlist Mathematics