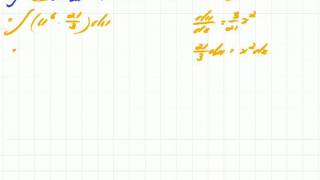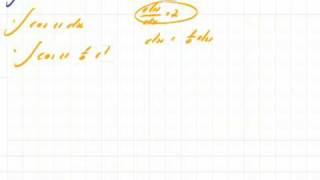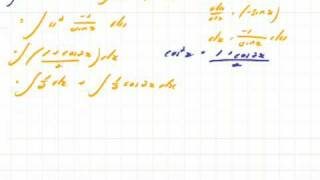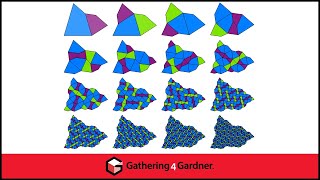
In geometry, a tile substitution is a method for constructing highly ordered tilings. Most importantly, some tile substitutions generate aperiodic tilings, which are tilings whose prototiles do not admit any tiling with translational symmetry. The most famous of these are the Penrose tilings. Substitution tilings are special cases of finite subdivision rules, which do not require the tiles to be geometrically rigid. (Wikipedia).
Integration 8 The Substitution Rule in Integration Part 2 Example 9
Working through an example using substitution in integration.
From playlist Integration
Integration 8 The Substitution Rule in Integration Part 2 Example 8
Working through an example using substitution in integration.
From playlist Integration
Integration 8 The Substitution Rule in Integration Part 2 Example 6
Working through an example using substitution in integration.
From playlist Integration
Integration 8 The Substitution Rule in Integration Part 2 Example 1
Working through an example of substitution in integration.
From playlist Integration
Integration 8 The Substitution Rule in Integration Part 2 Example 7
Working through an example using substitution in integration.
From playlist Integration
Expanding and Factorising (4 of 4: What is Substitution?)
More resources available at www.misterwootube.com
From playlist Formulae and Equations
Integration 12_5_3 Trigonometric Integration.mov
Another example of trigonometric substitution.
From playlist Integration
Ex 2: Solve a System of Equations Using Substitution
This video provides an example of how to solve a system of linear equation using the substitution method. Complete Library: http://www.mathispower4u.com Search by Topic: http://www.mathispower4u.wordpress.com
From playlist Solving Systems of Equations Using Substitution
Nathalie Priebe Frank : Introduction to hierarchical tiling dynamical systems
Abstract: These lectures introduce the dynamical systems approach to tilings of Euclidean space, especially quasicrystalline tilings that have been constructed using a 'supertile method'. Because tiling dynamics parallels one-dimensional symbolic dynamics, we discuss this case as well, hig
From playlist Dynamical Systems and Ordinary Differential Equations
60 years of dynamics and number expansions - 10 December 2018
http://crm.sns.it/event/441/ 60 years of dynamics and number expansions Partially supported by Delft University of Technology, by Utrecht University and the University of Pisa It has been a little over sixty years since A. Renyi published his famous article on the dynamics of number expa
From playlist Centro di Ricerca Matematica Ennio De Giorgi
Integration 8 The Substitution Rule in Integration Part 2 Example 5
Working through an example using the substitution rule in integration.
From playlist Integration
Boris Solomyak: Lecture on Delone sets and Tilings
Abstract: In this lecture we focus on selected topics around the themes: Delone sets as models for quasicrystals, inflation symmetries and expansion constants, substitution Delone sets and tilings, and associated dynamical systems. Recording during the Jean-Morlet chair research school "T
From playlist Dynamical Systems and Ordinary Differential Equations
Counting Integer Points in Polygons with Negative Numbers | A 'moral' Intro to Generating Functions
Turn on the subtitles for the BEST experience. :) 0:00 - Introduction 5:17 - Section 1: The What and Why of Generating Functions 15:18 - Section 2: Finding GFs for Lattice Counting Functions 34:11 - Section 3: Substituting Negative Numbers 47:46 - Section 4: The Finale 58:09 - Conclusion
From playlist Summer of Math Exposition 2 videos
A previously unknown substitution tiling can be built from powers 0 to 4 of a complex root of x^3 == x^2 + 1. In this talk, Ed Pegg discusses how algebraic numbers and barycentric coordinates can be used to explore both a new branch of tiling systems and simple representations for some old
From playlist Wolfram Technology Conference 2020
Ed Pegg - New Substitution Tilings - CoM Apr 2021
A previously unknown substitution tiling can be directly built from powers 0 to 4 of a complex root of x^3 = x^2+1, the supergolden ratio. This talk will discuss new and old tiling systems and the algebraic roots behind them. Ed Pegg Jr is a long time recreational mathematician who worked
From playlist Celebration of Mind 2021
Kaapi with Kuriosity: Tilings (ONLINE) by Mahuya Datta
Kaapi with Kuriosity Tilings (ONLINE) Speaker: Mahuya Datta (Indian Statistical Institute, Kolkata) When: 4:00 pm to 5:30 pm Sunday, 27 March 2022 Where: Zoom meeting and Livestream on ICTS YouTube channel Abstract: Tiling is a way of arranging plane shapes so that they completely co
From playlist Kaapi With Kuriosity (A Monthly Public Lecture Series)
What We've Learned from NKS Chapter 5: Two Dimensions and Beyond
In this episode of "What We've Learned from NKS", Stephen Wolfram is counting down to the 20th anniversary of A New Kind of Science with [another] chapter retrospective. If you'd like to contribute to the discussion in future episodes, you can participate through this YouTube channel or th
From playlist Science and Research Livestreams
Integration 12_5_4 Trigonometric Integration.mov
Another example of trigonometric substitution.
From playlist Integration
Robert Fathauer - Tessellations: Mathematics, Art, and Recreation - CoM Apr 2021
A tessellation, also known as a tiling, is a collection of shapes (tiles) that fit together without gaps or overlaps. Tessellations are a topic of mathematics research as well as having many practical applications, the most obvious being the tiling of floors and other surfaces. There are n
From playlist Celebration of Mind 2021
