Arctan(1) + Arctan(2) + Arctan(3) = π
From playlist Trigonometry TikToks

Caustics of fronts and the arborealization conjecture - Daniel Alvarez-Gavela
Short talks by postdoctoral members Topic: Caustics of fronts and the arborealization conjecture Speaker: Daniel Alvarez-Gavela Affiliation: Member, School of Mathematics Date: September 25, 2018 For more video please visit http://video.ias.edu
From playlist Mathematics

Separation of Variables - Cylindrical Coordinates (Part 1)
A vibrating drum can be described by a partial differential equation - the wave equation. For a circular drum, the solution for the vibration can be found by using the technique of Separation of Variables in Cylindrical coordinates.
From playlist Mathematical Physics II Uploads

Towards Morse theory of dispersion relations - Gregory Berkolaiko
Mathematical Physics Seminar Topic: Towards Morse theory of dispersion relations Speaker: Gregory Berkolaiko Affiliation: Texas A&M University Date: April 20, 2022 The question of optimizing an eigenvalue of a family of self-adjoint operators that depends on a set of parameters arises i
From playlist Mathematics
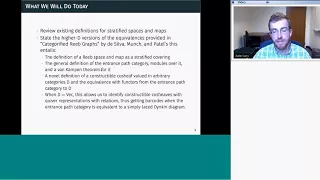
Ryan Grady - Persistence over the Circle
38th Annual Geometric Topology Workshop (Online), June 15-17, 2021 Ryan Grady, Montana State University Title: Persistence over the Circle Abstract: In this talk we will construct algebraic topological invariants of persistence modules on the circle. In particular, we will discuss the K-t
From playlist 38th Annual Geometric Topology Workshop (Online), June 15-17, 2021
Robert Ghrist, Lecture 2: Topology Applied II
27th Workshop in Geometric Topology, Colorado College, June 11, 2010
From playlist Robert Ghrist: 27th Workshop in Geometric Topology

Introduction to Spherical Harmonics
Using separation of variables in spherical coordinates, we arrive at spherical harmonics.
From playlist Quantum Mechanics Uploads

Separation of variables and the Schrodinger equation
A brief explanation of separation of variables, application to the time-dependent Schrodinger equation, and the solution to the time part. (This lecture is part of a series for a course based on Griffiths' Introduction to Quantum Mechanics. The Full playlist is at http://www.youtube.com/
From playlist Mathematical Physics II - Youtube

On The Work Of Narasimhan and Seshadri (Lecture 3) by Edward Witten
Program Quantum Fields, Geometry and Representation Theory 2021 (ONLINE) ORGANIZERS: Aswin Balasubramanian (Rutgers University, USA), Indranil Biswas (TIFR, india), Jacques Distler (The University of Texas at Austin, USA), Chris Elliott (University of Massachusetts, USA) and Pranav Pandi
From playlist Quantum Fields, Geometry and Representation Theory 2021 (ONLINE)

The Morse Complex on Singular Spaces - Graeme Wilkin
Glimpses of Mathematics, Now and Then: A Celebration of Karen Uhlenbeck's 80th Birthday Topic: The Morse Complex on Singular Spaces Speaker: Graeme Wilkin Affiliation: University of York Date: September 17, 2022 Morse theory is a beautiful subject with a long history, which includes sign
From playlist Glimpses of Mathematics, Now and Then: A Celebration of Karen Uhlenbeck's 80th Birthday

Higher ribbon graphs - David Nadler
Princeton/IAS Symplectic Geometry Seminar Topic: Higher ribbon graphs Speaker: David Nadler Affiliation: University of California, Berkeley Date: March 12, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Mikhail Katz (7/14/20): Collapsing surfaces
The collapse of Riemannian manifolds M and more general metric spaces to a lower-dimensional space X in the presence of a uniform lower bound on the Alexandrov curvature is a much-studied subject where many open questions remain. We examine the case of surfaces M collapsing to circles or s
From playlist AATRN 2021

PUSHING A GAUSSIAN TO THE LIMIT
Integrating a gaussian is everyones favorite party trick. But it can be used to describe something else. Link to gaussian integral: https://www.youtube.com/watch?v=mcar5MDMd_A Link to my Skype Tutoring site: dotsontutoring.simplybook.me or email dotsontutoring@gmail.com if you have ques
From playlist Math/Derivation Videos

(PP 6.3) Gaussian coordinates does not imply (multivariate) Gaussian
An example illustrating the fact that a vector of Gaussian random variables is not necessarily (multivariate) Gaussian.
From playlist Probability Theory

(PP 6.2) Multivariate Gaussian - examples and independence
Degenerate multivariate Gaussians. Some sketches of examples and non-examples of Gaussians. The components of a Gaussian are independent if and only if they are uncorrelated.
From playlist Probability Theory

Emil Saucan (7/29/22): Discrete Morse Theory, Persistent Homology and Forman-Ricci Curvature
Abstract: It was observed experimentally that Persistent Homology of networks and hypernetworks schemes based on Forman's discrete Morse Theory and on the 1-dimensional version of Forman's Ricci curvature not only both perform well, but they also produce practically identical results. We s
From playlist Applied Geometry for Data Sciences 2022