
Multivariable Calculus | The equation of a sphere.
We derive the equation of a sphere in R^3 and look at some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Common Surfaces in Multivariable Calculus

Equation of Sphere with Radius 3 and Center (3, -1, 0)
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Equation of Sphere with Radius 3 and Center (3, -1, 0)
From playlist Calculus

Calculus 3: Graphing in 3-D Basic Shapes (4 of 9) Equation of a Sphere
Visit http://ilectureonline.com for more math and science lectures! In this video I will find the equation of a sphere in 3 dimensional space using the line segment and radius equations in 3 dimensional space. Next video in the series can be seen at: https://youtu.be/6XLYbuohq98
From playlist CALCULUS 3 CH 3.2 GRAPHING IN 3-D

Understanding the Volume of a Sphere Formula [Using High School Geometry]
Deriving the volume of a sphere formula. (4/3)πr(cubed) gives you the volume of a sphere, but where does the formula come from? Here is a simple explanation using geometry and algebra. The volume of a sphere is the measurement of the space it can occupy. A sphere is a three-dimensional sha
From playlist Math formulas, proofs, ideas explained

The video explains how to determine the center and radius of a sphere. http://mathispower4u.yolasite.com/
From playlist Vectors

Calculus 3: Graphing in 3-D Basic Shapes (5 of 9) The General Equation of a Sphere
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain how can we tell if a given equation, x^2+y^2+z^2-2x-4y+6z+10=0, is an equation of a sphere, a point, or nothing at all? Next video in the series can be seen at: https://youtu.be/8uYRS0wN3iI
From playlist CALCULUS 3 CH 3.2 GRAPHING IN 3-D

Vector Equations of Spheres (1 of 2: Tangential spheres)
More resources available at www.misterwootube.com
From playlist Further Work with Vectors

Example of Equation of a Sphere
Multivariable Calculus: A sphere has center (0,3,4) and passes through the point (1,1,1). Find the points on the sphere above the point (sqrt(6), 1) in the xy-plane. For more videos like this one, please visit the Multivariable Calculus playlist at my channel.
From playlist Calculus Pt 7: Multivariable Calculus

This lecture was held by Abel Laureate John Milnor at The University of Oslo, May 25, 2011 and was part of the Abel Prize Lectures in connection with the Abel Prize Week celebrations. Program for the Abel Lectures 2011 1. "Spheres" by Abel Laureate John Milnor, Institute for Mathematical
From playlist Abel Lectures

[BOURBAKI 2019] Manolescu’s work on the triangulation conjecture - Stipsicz - 15/06/19
András STIPSICZ Manolescu’s work on the triangulation conjecture The triangulation conjecture (asking whether a manifold is necessarily a simplicial complex) has been recently resolved in the negative by Ciprian Manolescu. His proof is based on work of Galweski–Stern and Matumoto, reduci
From playlist BOURBAKI - 2019

Henry Adams (10/11/17): Metric reconstruction via optimal transport
Given a sample of points X in a metric space M and a scale parameter r, the Vietoris-Rips simplicial complex VR(X;r) is a standard construction to attempt to recover M from X up to homotopy type. A deficiency of this approach is that VR(X;r) is not metrizable if it is not locally finite, a
From playlist AATRN 2017
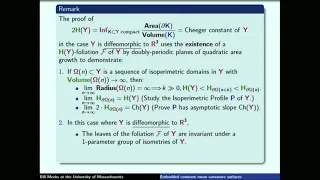
Progress in the theory of CMC surfaces in locally homgeneous 3-manifolds X - William Meeks
Workshop on Mean Curvature and Regularity Topic: Progress in the theory of CMC surfaces in locally homgeneous 3-manifolds X Speaker: William Meeks Affiliation: University of Massachusetts; Member, School of Mathematics Date: November 9, 2018 For more video please visit http://video.ias.e
From playlist Workshop on Mean Curvature and Regularity

“Closed Geodesics on Surfaces Pt.2” - Nancy Hingston
Nancy Hingston TCNJ “Closed geodesics on surfaces” Wednesday May 18
From playlist Mathematics

8ECM Invited Lecture: Burak Özbağcı
From playlist 8ECM Invited Lectures
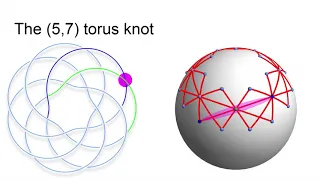
Knots, three-manifolds and instantons – Peter Kronheimer & Tomasz Mrowka – ICM2018
Plenary Lecture 11 Knots, three-manifolds and instantons Peter Kronheimer & Tomasz Mrowka Abstract: Over the past four decades, input from geometry and analysis has been central to progress in the field of low-dimensional topology. This talk will focus on one aspect of these developments
From playlist Plenary Lectures

On the existence of minimal Heegaard splittings - Dan Ketover
Variational Methods in Geometry Seminar Topic: On the existence of minimal Heegaard splittings Speaker: Dan Ketover Affiliation: Princeton University; Member, School of Mathematics Date: Oct 2, 2018 For more video please visit http://video.ias.edu
From playlist Variational Methods in Geometry

Spectral characterizations of Besse and Zoll Reeb flows - Marco Mazzucchelli
IAS/PU-Montreal-Tel-Aviv Symplectic Geometry Seminar Topic: Spectral characterizations of Besse and Zoll Reeb flows Speaker: Marco Mazzucchelli Affiliation: École normale supérieure de Lyon Date: May 8, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

The Work of Grigory Perelman - John Lott [ICM 2006]
slides for this talk: https://www.mathunion.org/fileadmin/IMU/Videos/ICM2006/tars/laudationes2006_perelman.pdf The Work of Grigory Perelman John Lott University of Maryland, USA https://www.mathunion.org/icm/icm-videos/icm-2006-videos-madrid-spain/icm-madrid-videos-22082006
From playlist Mathematics

Jessica Purcell: Structure of hyperbolic manifolds - Lecture 3
Abstract: In these lectures, we will review what it means for a 3-manifold to have a hyperbolic structure, and give tools to show that a manifold is hyperbolic. We will also discuss how to decompose examples of 3-manifolds, such as knot complements, into simpler pieces. We give conditions
From playlist Topology
