
Prerequisites of a smooth function.
From playlist Advanced Calculus / Multivariable Calculus

Manifolds 2.2 : Examples and the Smooth Manifold Chart Lemma
In this video, I introduce examples of smooth manifolds, such as spheres, graphs of smooth functions, real vectorspaces, linear map spaces, and the Grassmannian of real vectorspaces (G_k(V)). Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet Play
From playlist Manifolds
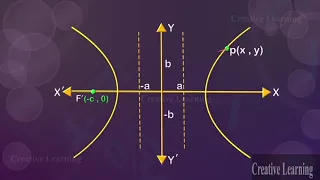
Hyperbola 3D Animation | Objective conic hyperbola | Digital Learning
Hyperbola 3D Animation In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other an
From playlist Maths Topics

This lecture is part of an online course on category theory. We define functors and give some examples of them. For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj51F9XZ_Ka4bLnQoxTdMx0AL
From playlist Categories for the idle mathematician

Smooth Transition Function in One Dimension | Smooth Transition Function Part 1
#SoME2 This video gives a detailed construction of transition function for various levels of smoothness. Sketch of proofs for 4 theorems regarding smoothness: https://kaba.hilvi.org/homepage/blog/differentiable.htm Faà di Bruno's formula: https://en.wikipedia.org/wiki/Fa%C3%A0_di_Bruno%2
From playlist Summer of Math Exposition 2 videos

Manifolds 2.3 : Smooth Maps and Diffeomorphisms
In this video, I introduce examples and properties of smooth maps, and show the invariance theorems for diffeomorphisms. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet Playlist :
From playlist Manifolds

Felix Klein Lecture 2022 part6
From playlist Felix Klein Lectures 2022

Daxin Xu - Parallel transport for Higgs bundles over p-adic curves
Faltings conjectured that under the p-adic Simpson correspondence, finite dimensional p-adic representations of the geometric étale fundamental group of a smooth proper p-adic curve X are equivalent to semi-stable Higgs bundles of degree zero over X. We will talk about an equivalence betwe
From playlist Franco-Asian Summer School on Arithmetic Geometry (CIRM)

David Ayala: Factorization homology (part 2)
The lecture was held within the framework of the Hausdorff Trimester Program: Homotopy theory, manifolds, and field theories and Introductory School (7.5.2015)
From playlist HIM Lectures 2015
Exploring those Hard-to-Visualize Calculus 3D Surfaces
https://www.geogebra.org/m/agmkusms
From playlist Calculus: Dynamic Interactives!

Jacob Lurie: A Riemann-Hilbert Correspondence in p-adic Geometry Part 2
At the start of the 20th century, David Hilbert asked which representations can arise by studying the monodromy of Fuchsian equations. This question was the starting point for a beautiful circle of ideas relating the topology of a complex algebraic variety X to the study of algebraic diffe
From playlist Felix Klein Lectures 2022

Robert Cass: Perverse mod p sheaves on the affine Grassmannian
28 September 2021 Abstract: The geometric Satake equivalence relates representations of a reductive group to perverse sheaves on an affine Grassmannian. Depending on the intended application, there are several versions of this equivalence for different sheaf theories and versions of the a
From playlist Representation theory's hidden motives (SMRI & Uni of Münster)

Algebraic Spaces and Stacks: Representabilty
We define what it means for a functor to be representable. We define what it means for a category to be representable.
From playlist Stacks
Surface with Square Cross Sections
Surface with square cross sections and modifiable base: https://www.geogebra.org/m/mcfmabak #GeoGebra #math #geometry #calculus #AugmentedReality
From playlist Calculus: Dynamic Interactives!

Generalized Conway Game of Life - SmoothLife4
Oscillatory structures are also possible.
From playlist SmoothLife

Marc Levine - "The Motivic Fundamental Group"
Research lecture at the Worldwide Center of Mathematics.
From playlist Center of Math Research: the Worldwide Lecture Seminar Series

Fractals are typically not self-similar
An explanation of fractal dimension. Help fund future projects: https://www.patreon.com/3blue1brown An equally valuable form of support is to simply share some of the videos. Special thanks to these supporters: https://3b1b.co/fractals-thanks And by Affirm: https://www.affirm.com/careers H
From playlist Explainers

Duality In Higher Categories IV by Pranav Pandit
PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics
From playlist Dualities in Topology and Algebra (Online)

