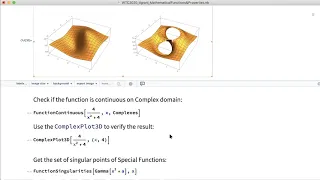
Singularity (mathematics)
In mathematics, a singularity is a point at which a given mathematical object is not defined, or a point where the mathematical object ceases to be well-behaved in some particular way, such as by lacking differentiability or analyticity. For example, the real function has a singularity at , where the numerical value of the function approaches so the function is not defined. The absolute value function also has a singularity at , since it is not differentiable there. The algebraic curve defined by in the coordinate system has a singularity (called a cusp) at . For singularities in algebraic geometry, see singular point of an algebraic variety. For singularities in differential geometry, see singularity theory. (Wikipedia).