
Simplicial complexes as expanders - Ori Parzanchevski
Ori Parzanchevski Institute for Advanced Study; Member, School of Mathematics February 4, 2014 Expanders are highly connected sparse graphs. Simplicial complexes are a natural generalization of graphs to higher dimension, and the notions of connectedness and expansion turn out to have inte
From playlist Mathematics

Simplicial complexes as expanders - Ori Parzanchevski
Simplicial complexes as expanders - Ori Parzanchevski Ori Parzanchevski Institute for Advanced Study; Member, School of Mathematics January 28, 2014 Expanders are highly connected sparse graphs. Simplicial complexes are a natural generalization of graphs to higher dimension, and the notio
From playlist Mathematics

The Simplicial Model of Univalence - Peter Lumsdaine
Peter Lumsdaine Dalhousie University; Member, School of Mathematics, IAS December 6, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics

The Simplicial Model of Univalence - Chris Kapulkin
Chris Kapulkin Visiting Student, School of Mathematics November 29, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics

Simplices and simplicial complexes | Algebraic Topology | NJ Wildberger
Simplices are higher dimensional analogs of line segments and triangle, such as a tetrahedron. We begin this lecture by discussing convex combinations and convex hulls, and showing a natural hierarchy from point to line segment to triangle to tetrahedron. Each of these also has a standard
From playlist Algebraic Topology
Kan Simplicial Set Model of Type Theory - Peter LeFanu Lumsdaine
Peter LeFanu Lumsdaine Dalhousie University; Member, School of Mathematics October 25, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics
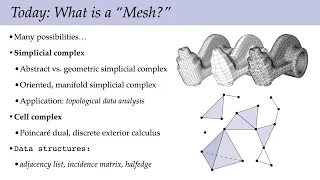
Lecture 2A: What is a "Mesh?" (Discrete Differential Geometry)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg
From playlist Discrete Differential Geometry - CMU 15-458/858

Omer Bobrowski: Random Simplicial Complexes II
A simplicial complex is a collection of vertices, edges, triangles, tetrahedra and higher dimensional simplexes glued together. In other words, it is a higher-dimensional generalization of a graph. In recent years there has been a growing effort in developing the theory of random simplicia
From playlist Workshop: High dimensional spatial random systems

Simplify a large numeric expression by applying the order of operations
👉 Learn how to simplify mathematics expressions. A mathematis expression is a finite combination of numbers and symbols formed following a set of operations or rules. To simplify a mathematics expression means to reduce the expression into simpler form. For expressions having parenthesis
From playlist Simplify Expressions Using Order of Operations

Johnathan Bush (11/5/21): Maps of Čech and Vietoris–Rips complexes into euclidean spaces
We say a continuous injective map from a topological space to k-dimensional euclidean space is simplex-preserving if the image of each set of at most k+1 distinct points is affinely independent. We will describe how simplex-preserving maps can be useful in the study of Čech and Vietoris–Ri
From playlist Vietoris-Rips Seminar

Henry Adams (10/11/17): Metric reconstruction via optimal transport
Given a sample of points X in a metric space M and a scale parameter r, the Vietoris-Rips simplicial complex VR(X;r) is a standard construction to attempt to recover M from X up to homotopy type. A deficiency of this approach is that VR(X;r) is not metrizable if it is not locally finite, a
From playlist AATRN 2017

Jennifer WILSON - High dimensional cohomology of SL_n(Z) and its principal congruence subgroups 3
Group cohomology of arithmetic groups is ubiquitous in the study of arithmetic K-theory and algebraic number theory. Rationally, SL_n(Z) and its finite index subgroups don't have cohomology above dimension n choose 2. Using Borel-Serre duality, one has access to the high dimensions. Church
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Francisco Martinez Figueroa (8/19/22): Chromatic number of G-Borsuk graphs
The Borsuk graph has vertex set the sphere S^d, and edges x∼y whenever x and y are ϵ-almost antipodal. It is well known that when epsilon is small, its chromatic number is d+2, which follows from the topology of S^d via Borsuk-Ulam's Theorem. Given a finite group G acting freely over a com
From playlist Vietoris-Rips Seminar

Simplicial descent for Chekanov-Eliashberg dg-algebras - Johan Asplund
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Topic: Simplicial descent for Chekanov-Eliashberg dg-algebras Speaker: Johan Asplund Affiliation: Uppsala Date: December 17, 2021 In this talk we introduce a type of surgery decomposition of Weinstein manifolds we c
From playlist Mathematics

Lecture 2B: Introduction to Manifolds (Discrete Differential Geometry)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg
From playlist Discrete Differential Geometry - CMU 15-458/858

Fedor Manin (3/19/22): Linear nullhomotopies of maps to spheres
I will explain some aspects of how to build (null)homotopies of maps to simply connected spaces with controlled Lipschitz constant. Most of the difficulties appear already in the case of maps between spheres, where the result is as follows: every nullhomotopic, $L$-Lipschitz map $S^m \to
From playlist Vietoris-Rips Seminar

Periodic Foams and Manifolds - Frank Lutz
Frank Lutz Technische Universitat Berlin March 2, 2011 WORKSHOP ON TOPOLOGY: IDENTIFYING ORDER IN COMPLEX SYSTEMS For more videos, visit http://video.ias.edu
From playlist Mathematics

Jennifer WILSON - High dimensional cohomology of SL_n(Z) and its principal congruence subgroups 2
Group cohomology of arithmetic groups is ubiquitous in the study of arithmetic K-theory and algebraic number theory. Rationally, SL_n(Z) and its finite index subgroups don't have cohomology above dimension n choose 2. Using Borel-Serre duality, one has access to the high dimensions. Church
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory
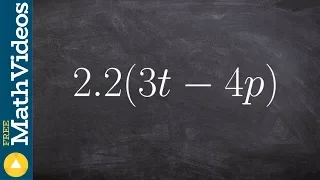
Simplifying an expression using distributive property ex 6, 2.2(3t - 4p)
👉 Learn how to simplify mathematics expressions. A mathematis expression is a finite combination of numbers and symbols formed following a set of operations or rules. To simplify a mathematics expression means to reduce the expression into simpler form. For expressions having parenthesis
From playlist Simplify Expressions Using Order of Operations

Thorben Kastenholz: Simplicial Volume of Total Spaces of Fiber Bundles
Thorben Kastenholz, University of Goettingen Title: Simplicial Volume of Total Spaces of Fiber Bundles It is a classical result that manifolds that are total spaces of fiber bundles, whose fiber has amenable fundamental group, have vanishing simplicial volume. In this talk I will explore t
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022