
Abstract Algebra: Group actions are defined as a formal mechanism that describes symmetries of a set X. A given group action defines an equivalence relation, which in turn yields a partition of X into orbits. Orbits are also described as cosets of the group. U.Reddit course materials a
From playlist Abstract Algebra

Inner & Outer Semidirect Products Derivation - Group Theory
Semidirect products are a very important tool for studying groups because they allow us to break a group into smaller components using normal subgroups and complements! Here we describe a derivation for the idea of semidirect products and an explanation of how the map into the automorphism
From playlist Group Theory

Group actions in abstract algebra
In this first video on group actions, I use an example of some previous work on the symmetric group to give you some intuition about group actions. Beware when reading your textbook. It is probably unnecessary difficult just due to the dot notation that is used when describing group acti
From playlist Abstract algebra

Walter van Suijlekom: Semigroup of inner perturbations in Non Commutative Geometry
Starting with an algebra, we define a semigroup which extends the group of invertible elements in that algebra. As we will explain, this semigroup describes inner perturbations of noncommutative manifolds, and has applications to gauge theories in physics. We will present some elementary e
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

What is a Group Action? : A Group as a Category and The Skeleton Operation ☠
This week I try to take a more Categorical approach to answering and expanding upon the question of "what is a group action". Along the way I'll go over thinking about a group as a category and eventually hit on the skeleton operation on a category and use it to present an example of the c
From playlist The New CHALKboard

Group theory 7: Semidirect products
This is lecture 7 of an online course on group theory. It covers semidirect products and uses them to classify groups of order 6.
From playlist Group theory

In this video I demonstrate an example of a non-faithful group actions, where the identity permutation is actually mapped to by all the elements in the group set. Another example shows you how group actions involving a group set on itself gives rise to group element composition as we see
From playlist Abstract algebra

Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra

On the structure of quantum Markov semigroups - F. Fagnola - PRACQSYS 2018 - CEB T2 2018
Franco Fagnola (Department of Mathematics, Politecnico di Milano, Italy) / 06.07.2018 On the structure of quantum Markov semigroups We discuss the relationships between the decoherence-free subalgebra and the structure of the fixed point subalgebra of a quantum Markov semigroup on B(h) w
From playlist 2018 - T2 - Measurement and Control of Quantum Systems: Theory and Experiments

Inner Semidirect Product Example: Dihedral Group
Semidirect products explanation: https://youtu.be/Pat5Qsmrdaw Semidirect products are very useful in group theory. To understand why, it's helpful to see an example. Here we show how to write the dihedral group D_2n as a semidirect product, and how we can describe that purely using cyclic
From playlist Group Theory

BAG1.4. Toric Varieties 4 - Spec(R) and Affine Semigroups
Basic Algebraic Geometry: In this part, we introduce Spec(R) and affine semigroups. This allows us to give yet another characterization of affine toric varieties in terms of affine semigroups.
From playlist Basic Algebraic Geometry

Markus Haase : Operators in ergodic theory - Lecture 3 : Compact semigroups and splitting theorems
Abstract : The titles of the of the individual lectures are: 1. Operators dynamics versus base space dynamics 2. Dilations and joinings 3. Compact semigroups and splitting theorems Recording during the thematic meeting : "Probabilistic Aspects of Multiple Ergodic Averages " the December 8
From playlist Dynamical Systems and Ordinary Differential Equations

Concentration of quantum states from quantum functional (...) - N. Datta - Workshop 2 - CEB T3 2017
Nilanjana Datta / 24.10.17 Concentration of quantum states from quantum functional and transportation cost inequalities Quantum functional inequalities (e.g. the logarithmic Sobolev- and Poincaré inequalities) have found widespread application in the study of the behavior of primitive q
From playlist 2017 - T3 - Analysis in Quantum Information Theory - CEB Trimester

"New Paradigms in Invariant Theory" - Roger Howe, Yale University [2011]
HKUST Institute for Advanced Study Distinguished Lecture New Paradigms in Invariant Theory Speaker: Prof Roger Howe, Yale University Date: 13/6/2011 Video taken from: http://video.ust.hk/Watch.aspx?Video=6A41D5F6B1A790DC
From playlist Mathematics
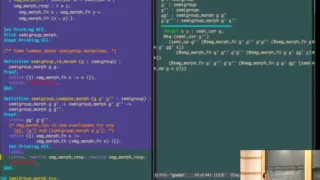
Type Classes for Mathematical Formalizations in Coq - Matthieu Sozeau
Matthieu Sozeau INRIA Paris; Member, School of Mathematics October 3, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics

Graeme Segal: Wick rotation and the positivity of energy in quantum field theory
Talk by Graeme Segal in Global Noncommutative Geometry Seminar (Americas) on December 17, 2021. https://globalncgseminar.org/talks/tba-19/
From playlist Global Noncommutative Geometry Seminar (Americas)

An asymptotic for the growth of Markoff-Hurwitz tuples - Ryan Ronan
Special Seminar Topic: An asymptotic for the growth of Markoff-Hurwitz tuples Speaker: Ryan Ronan Affiliation: Baruch College, The City University of New York Date: December 8, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Joachim Cuntz: Semigroup C*-algebras and toric varieties
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. The coordinate ring of a toric variety is the semigroup ring of a finitely generated subsemigroup of Zn. Such semigroups have the interesting feature that their family of constructib
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Jean Bourgain - 1/2 The orbital circle method and applications...
Jean Bourgain - The orbital circle method and applications / Toral eigenfuctions and their nodal sets
From playlist École d'été 2014 - Théorie analytique des nombres

Visual Group Theory, Lecture 5.1: Groups acting on sets
Visual Group Theory, Lecture 5.1: Groups acting on sets When we first learned about groups as collections of actions, there was a subtle but important difference between actions and configurations. This is the tip of the iceberg of a more general and powerful concept of a group action. Ma
From playlist Visual Group Theory