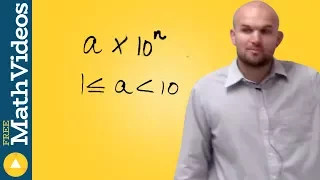
What is the definition of scientific notation
👉 Learn about scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is the number of digits up to t
From playlist Scientific Notation | Learn About

MIT 3.60 | Lec 10b: Symmetry, Structure, Tensor Properties of Materials
Part 2: 3D Symmetries, Point Groups View the complete course at: http://ocw.mit.edu/3-60F05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 3.60 Symmetry, Structure & Tensor Properties of Material

MIT 3.60 | Lec 4a: Symmetry, Structure, Tensor Properties of Materials
Part 1: 2D Symmetries View the complete course at: http://ocw.mit.edu/3-60F05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 3.60 Symmetry, Structure & Tensor Properties of Material

MIT 3.60 | Lec 8b: Symmetry, Structure, Tensor Properties of Materials
Part 2: Diffraction, 3D Symmetries View the complete course at: http://ocw.mit.edu/3-60F05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 3.60 Symmetry, Structure & Tensor Properties of Material

MIT 3.60 | Lec 14b: Symmetry, Structure, Tensor Properties of Materials
Part 2: Final Lecture on Symmetry: 3D Space Groups View the complete course at: http://ocw.mit.edu/3-60F05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 3.60 Symmetry, Structure & Tensor Properties of Material

MIT 3.60 | Lec 11a: Symmetry, Structure, Tensor Properties of Materials
Part 1: Point Groups View the complete course at: http://ocw.mit.edu/3-60F05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 3.60 Symmetry, Structure & Tensor Properties of Material

MIT 3.60 | Lec 11b: Symmetry, Structure, Tensor Properties of Materials
Part 2: Point Groups View the complete course at: http://ocw.mit.edu/3-60F05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 3.60 Symmetry, Structure & Tensor Properties of Material

MIT 3.60 | Lec 15a: Symmetry, Structure, Tensor Properties of Materials
Part 1: Space Group Notation and Tensors View the complete course at: http://ocw.mit.edu/3-60F05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 3.60 Symmetry, Structure & Tensor Properties of Material

R. Haslhofer - The moduli space of 2-convex embedded spheres
We investigate the topology of the space of smoothly embedded n-spheres in R^{n+1}, i.e. the quotient space M_n:=Emb(S^n,R^{n+1})/Diff(S^n). By Hatcher’s proof of the Smale conjecture, M_2 is contractible. This is a highly nontrivial theorem generalizing in particular the Schoenflies theor
From playlist Ecole d'été 2016 - Analyse géométrique, géométrie des espaces métriques et topologie

Raising a scientific number to the third power
👉 Learn how to multiply numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is
From playlist Scientific Notation
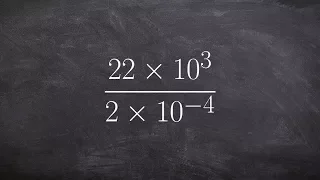
Dividing two numbers in scientific notation then rewriting answer in scientific notation
👉 Learn how to divide numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is t
From playlist Scientific Notation

This video explains how to convert between scientific notation and standard notation. Video content created Jenifer Bohart, William Meacham, Judy Sutor, and Donna Guhse from SCC (CC-BY 4.0)
From playlist Scientific Notation

Multiplying in scientific notation with negative exponents
👉 Learn how to multiply numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is
From playlist Scientific Notation
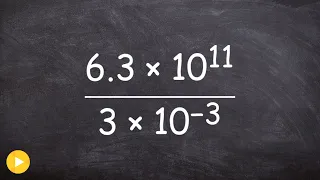
Learn how to divide two numbers in scientific notation
👉 Learn how to divide numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is t
From playlist Scientific Notation

Learn how to divide two numbers in scientific notation
👉 Learn how to divide numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is t
From playlist Scientific Notation

Multiplying two numbers in scientific notation
👉 Learn how to multiply numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is
From playlist Scientific Notation
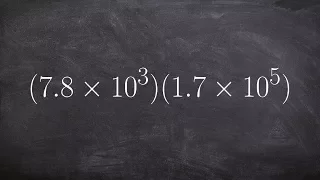
Multiplying two numbers in scientific notation
👉 Learn how to multiply numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is
From playlist Scientific Notation

TabletClass Math http://www.tabletclass.com . This explains interval notation and set builder notation. Set notation is used in more advance math like Pre-Calculus and higher.
From playlist Pre-Calculus / Trigonometry

Dividing two numbers in scientific notation
👉 Learn how to divide numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is t
From playlist Scientific Notation

Scientific Notation and Their Operations
Everything you need to know about scientific notation. Like what scientific notation and standard notation is, a detailed explanation of what the typical scientific notation template looks like. You'll learn how to convert from scientific notation to standard notation and from standard not
From playlist The Math You'll Use in Chemistry