Regularization by spectral filtering

Inverse problems | Mathematical analysis

Spectral regularization is any of a class of regularization techniques used in machine learning to control the impact of noise and prevent overfitting. Spectral regularization can be used in a broad range of applications, from deblurring images to classifying emails into a spam folder and a non-spam folder. For instance, in the email classification example, spectral regularization can be used to reduce the impact of noise and prevent overfitting when a machine learning system is being trained on a labeled set of emails to learn how to tell a spam and a non-spam email apart. Spectral regularization algorithms rely on methods that were originally defined and studied in the theory of ill-posed inverse problems (for instance, see) focusing on the inversion of a linear operator (or a matrix) that possibly has a bad condition number or an unbounded inverse. In this context, regularization amounts to substituting the original operator by a bounded operator called the "regularization operator" that has a condition number controlled by a regularization parameter, a classical example being Tikhonov regularization. To ensure stability, this regularization parameter is tuned based on the level of noise. The main idea behind spectral regularization is that each regularization operator can be described using spectral calculus as an appropriate filter on the eigenvalues of the operator that defines the problem, and the role of the filter is to "suppress the oscillatory behavior corresponding to small eigenvalues". Therefore, each algorithm in the class of spectral regularization algorithms is defined by a suitable filter function (which needs to be derived for that particular algorithm). Three of the most commonly used regularization algorithms for which spectral filtering is well-studied are Tikhonov regularization, Landweber iteration, and truncated singular value decomposition (TSVD). As for choosing the regularization parameter, examples of candidate methods to compute this parameter include the discrepancy principle, generalized cross validation, and the L-curve criterion. It is of note that the notion of spectral filtering studied in the context of machine learning is closely connected to the literature on function approximation (in signal processing). (Wikipedia).

Regularization 1

An introduction to regularization with weight decay.

From playlist Regularization

Regularization 2

Examples of regularization.

From playlist Regularization

Network Analysis. Lecture 9. Graph partitioning algorithms

Graph density. Graph pertitioning. Min cut, ratio cut, normalized and quotient cuts metrics. Spectral graph partitioning (normalized cut). Direct (spectral) modularity maximization. Multilevel recursive partitioning Lecture slides: http://www.leonidzhukov.net/hse/2015/networks/lectures/le

From playlist Structural Analysis and Visualization of Networks.

reaLD 3D glasses filter with a linear polarising filter

This is for a post on my blog: http://blog.stevemould.com

From playlist Everything in chronological order

2020.05.21 Sara van der Geer - Learning with total variation regularization

Consider the classical problem of learning a signal when observed with noise. One way to do this is to expand the signal in terms of basis functions and then try to learn the coefficients. The collection of basis functions is called a dictionary and the approach is sometimes called "synthe

From playlist One World Probability Seminar

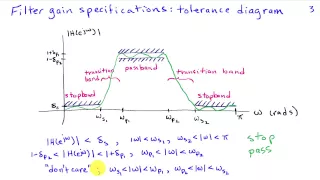
Introduction to Frequency Selective Filtering

http://AllSignalProcessing.com for free e-book on frequency relationships and more great signal processing content, including concept/screenshot files, quizzes, MATLAB and data files. Separation of signals based on frequency content using lowpass, highpass, bandpass, etc filters. Filter g

From playlist Introduction to Filter Design

Gilles Pagès: Optimal vector Quantization: from signal processing to clustering and ...

Abstract: Optimal vector quantization has been originally introduced in Signal processing as a discretization method of random signals, leading to an optimal trade-off between the speed of transmission and the quality of the transmitted signal. In machine learning, similar methods applied

From playlist Probability and Statistics

Principal Component Analysis

http://AllSignalProcessing.com for more great signal processing content, including concept/screenshot files, quizzes, MATLAB and data files. Representing multivariate random signals using principal components. Principal component analysis identifies the basis vectors that describe the la

From playlist Random Signal Characterization

Discrete noise filters

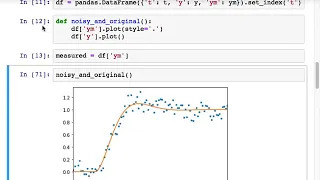
I discuss causal and non-causal noise filters: the moving average filter and the exponentially weighted moving average. I show how to do this filtering in Excel and Python

From playlist Discrete

Eighth Imaging & Inverse Problems (IMAGINE) OneWorld SIAM-IS Virtual Seminar Series Talk

Date: Wednesday, December 2, 10:00am EDT Speaker: Martin Burger, FAU Title: Nonlinear spectral decompositions in imaging and inverse problems Abstract: This talk will describe the development of a variational theory generalizing classical spectral decompositions in linear filters and si

From playlist Imaging & Inverse Problems (IMAGINE) OneWorld SIAM-IS Virtual Seminar Series

Lecture 3: Single-shot Multi-domain Camera

MIT MAS.531 Computational Camera and Photography, Fall 2009 Instructor: Roarke Horstmeyer View the complete course: https://ocw.mit.edu/courses/mas-531-computational-camera-and-photography-fall-2009/ YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP61pwA6paIRZ30q1sjLE8b6

From playlist MIT MAS.531 Computational Camera and Photography, Fall 2009

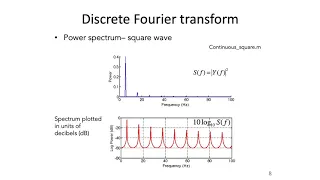
12: Spectral Analysis Part 2 - Intro to Neural Computation

MIT 9.40 Introduction to Neural Computation, Spring 2018 Instructor: Michale Fee View the complete course: https://ocw.mit.edu/9-40S18 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP61I4aI5T6OaFfRK2gihjiMm Covers Fourier transform pairs and power spectra, spectral esti

From playlist MIT 9.40 Introduction to Neural Computation, Spring 2018

Fabio Cipriani: Spectral densities and hypertrace in NCG

Talk in Global Noncommutative Geometry Seminar (Europe). 18 May 2022

From playlist Global Noncommutative Geometry Seminar (Europe)

Jeremy Hahn : Prismatic and syntomic cohomology of ring spectra

CONFERENCE Recording during the thematic meeting : « Chromatic Homotopy, K-Theory and Functors» the January 24, 2023 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Jean Petit Find this video and other talks given by worldwide mathematicians on CIR

From playlist Topology

Graph Convolutional and Isomorphism Networks

From playlist Machine Learning Streams

AMMI Course "Geometric Deep Learning" - Lecture 8 (Groups & Homogeneous spaces) - Taco Cohen

Video recording of the course "Geometric Deep Learning" taught in the African Master in Machine Intelligence in July-August 2021 by Michael Bronstein (Imperial College/Twitter), Joan Bruna (NYU), Taco Cohen (Qualcomm), and Petar Veličković (DeepMind) Lecture 8: Group convolution • Regular

From playlist AMMI Geometric Deep Learning Course - First Edition (2021)

Optimal machine learning with stochastic projections (...) - Rosasco - Workshop 3 - CEB T1 2019

Lorenzo Rosasco (MIT-IIT) / 03.04.2019 Optimal machine learning with stochastic projections and regularization. Projecting data in low dimensions is often key to scale machine learning to large high-dimensional data-sets. In this talk we will take take a statistical learning tour of cla

From playlist 2019 - T1 - The Mathematics of Imaging

Can You Solve This Astronomical Riddle?

In this video we look at one of the greatest astronomy riddles in history. A special thank you to Dr. Christian Sasse for all your help with this video, as well as the people of Siding Spring Observatory who made my time there so pleasant. If you'd like to learn how to make your own sp

From playlist Physics

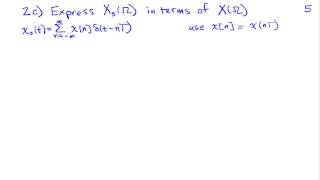
Frequency Domain Interpretation of Sampling

http://AllSignalProcessing.com for more great signal-processing content: ad-free videos, concept/screenshot files, quizzes, MATLAB and data files. Analysis of the effect of sampling a continuous-time signal in the frequency domain through use of the Fourier transform.

From playlist Sampling and Reconstruction of Signals

Xavier Bresson: "Convolutional Neural Networks on Graphs"

New Deep Learning Techniques 2018 "Convolutional Neural Networks on Graphs" Xavier Bresson, Nanyang Technological University, Singapore Abstract: Convolutional neural networks have greatly improved state-of-the-art performances in computer vision and speech analysis tasks, due to its hig

From playlist New Deep Learning Techniques 2018

Regularization by spectral filtering

Related pages