
Find a Particular Solution to a Nonhomgeneous DE Using Variation of Parameters
This video explains how to determine a particular solution to a linear second order differential equation using the method of variation of parameters. http://mathispower4u.com
From playlist Linear Second Order Nonhomogeneous Differential Equations: Variation of Parameters

Multivariable Calculus | Definition of partial derivatives.
We give the definition of the partial derivative of a function of more than one variable. In addition, we present some examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Multivariable Calculus

Derive the Variation of Parameters Formula to Solve Linear Second Order Nonhomogeneous DEs
This video derives or proves the variation of parameters formula used to find a particular solution and solve linear second order nonhomogeneous differential equations. Site: http://mathispower4u.com
From playlist Linear Second Order Nonhomogeneous Differential Equations: Variation of Parameters

Pre-Calculus - Types of variation
In this video I'll introduce the basic types of variation like direct, inverse, and joint variation. Near the end I'll also talk about combined variation where we put these basic forms together. Remember to see how the variable are connected for a clue on the type of variation. For more
From playlist Pre-Calculus

Leonid Potyagailo - Similar Relatively hyperbolic actions of a group
Leonid Potyagailo (Université de Lille 1, France) This is a joint work with Victor Gerasimov (University of Belo Horisonte, Brasil). Let a discrete group $G$ possess two convergence actions by homeomorphisms on compacta $X$ and $Y$. Consider the following question: does there exist a con
From playlist T1-2014 : Random walks and asymptopic geometry of groups.

Proof that every Differentiable Function is Continuous
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys A proof that every differentiable function is continuous.
From playlist Calculus

Algebraic Ending Laminations and Quasiconvexity by Mahan Mj
Surface Group Representations and Geometric Structures DATE: 27 November 2017 to 30 November 2017 VENUE:Ramanujan Lecture Hall, ICTS Bangalore The focus of this discussion meeting will be geometric aspects of the representation spaces of surface groups into semi-simple Lie groups. Classi
From playlist Surface Group Representations and Geometric Structures

A New Cubulation Theorem for Hyperbolic Groups- Daniel Groves
Daniel Groves University of Illinois, Chicago October 27, 2015 https://www.math.ias.edu/seminars/abstract?event=83384 We prove that if a hyperbolic group G acts cocompactly on a CAT(0) cube complexes and the cell stabilizers are quasiconvex and virtually special, then G is virtually spec
From playlist Geometric Structures on 3-manifolds

Partial Implicit Differentiation
http://mathispower4u.wordpress.com/
From playlist Functions of Several Variables - Calculus

Introduction to Direct Variation, Inverse Variation, and Joint Variation
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Introduction to Direct Variation, Inverse Variation, and Joint Variation
From playlist 3.7 Modeling Using Variation

Irène Waldspurger: Rank optimality for the Burer-Monteiro factorization
The Burer-Monteiro factorization is a classical heuristic used to speed up the solving of large scale semidefinite programs when the solution is expected to be low rank: One writes the solution as the product of thinner matrices, and optimizes over the (low-dimensional) factors instead of
From playlist Control Theory and Optimization
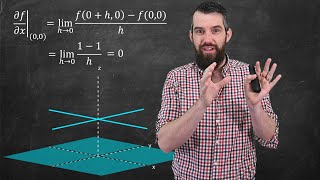
Continuity vs Partial Derivatives vs Differentiability | My Favorite Multivariable Function
In single variable calculus, a differentiable function is necessarily continuous (and thus conversely a discontinuous function is not differentiable). In multivariable calculus, you might expect a similar relationship with partial derivatives and continuity, but it turns out this is not th

Calculus of Variations ft. Flammable Maths
Flammable Maths: https://www.youtube.com/channel/UCtAIs1VCQrymlAnw3mGonhw Leibnitz Rule: https://www.youtube.com/watch?v=wkh1Y7R1sOw This video is an introduction to the calculus of variations. We go over what variational calculus is trying to solve, and derive the Euler-Lagrange equatio
From playlist Analysis

The Palais-Smale Theorem and the Solution of Hilbert’s 23 Problem - Karen Uhlenbeck
Members' Seminar Topic: The Palais-Smale Theorem and the Solution of Hilbert’s 23 Problem Speaker: Karen Uhlenbeck Affiliation: The University of Texas at Austin; Distinguished Visiting Professor, School of Mathematics Date: April 6, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Lec 23 | MIT 18.086 Mathematical Methods for Engineers II
Calculus of Variations / Weak Form View the complete course at: http://ocw.mit.edu/18-086S06 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 18.086 Mathematical Methods for Engineers II, Spring '06

Soviet Era Math Book for Beginners and Mathematical Experts
This book states that it is written with beginners in mind but it can also be of use to expert mathematicians. The first half of the book is on Differential Equations and the second half is on the Calculus of Variations. In this video I will show you this book and I will also solve a diffe
From playlist Book Reviews
A Taste of Calculus of Variations
Dirichlet's Principle In this video, I give you a taste of calculus of variations by illustrating Dirichlet's principle, which says that a function u is a minimizer of a certain Dirichlet energy (kinetic + potential energy) if and only if u solves Poisson's equation. This is a neat way of
From playlist Partial Differential Equations

Karen Uhlenbeck: Some Thoughts on the Calculus of Variations
Abstract: I will talk about some of the classic problems in the calculus of variations, and describe some of the mathematics which was developed to solve them. We will begin with the Greeks and end with some of the tantalizing problems of today. This lecture was given by the 2019 Abel Lau
From playlist Karen K. Uhlenbeck

