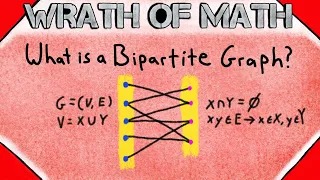
What is a Bipartite Graph? | Graph Theory
What is a bipartite graph? We go over it in today’s lesson! I find all of these different types of graphs very interesting, so I hope you will enjoy this lesson. A bipartite graph is any graph whose vertex set can be partitioned into two disjoint sets (called partite sets), such that all e
From playlist Graph Theory

What are Complete Bipartite Graphs? | Graph Theory, Bipartite Graphs
What are complete bipartite graphs? We'll define complete bipartite graphs and show some examples and non-examples in today's video graph theory lesson! Remember a graph G = (V, E) is bipartite if the vertex set V can be partitioned into two sets V1 and V2 (called partite sets) such that
From playlist Graph Theory

Bipartite Graphs with Isolated Vertices | Graph Theory, Complete Bipartite Graphs
We know what a bipartite graph is, and we know about complete bipartite graphs. But how do these definitions work with isolated vertices that have no neighbors? We'll go over just that in today's graph theory lesson! Remember that a bipartite graph is a graph whose vertices that can be pa
From playlist Graph Theory

OCR MEI MwA D: Graph Theory: 07 Bipartite Graphs
https://www.buymeacoffee.com/TLMaths Navigate all of my videos at https://sites.google.com/site/tlmaths314/ Like my Facebook Page: https://www.facebook.com/TLMaths-1943955188961592/ to keep updated Follow me on Instagram here: https://www.instagram.com/tlmaths/ Many, MANY thanks to Dea
From playlist OCR MEI MwA D: Graph Theory

From playlist Graph Theory
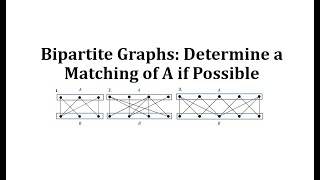
Bipartite Graphs: Determine a Matching of A if Possible
This video explains how to determine a matching of A in a bipartite and how to use Hall's Marriage theorem to explain why there I not a matching of A in a graph. mathispower4u.com
From playlist Graph Theory (Discrete Math)
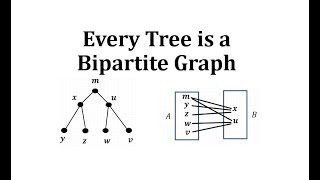
Every Tree is a Bipartite Graph
This video explains how to show that a tree is a bipartite graph. mathispower4u.com
From playlist Graph Theory (Discrete Math)

Bipartite Graphs and Named Graphs
The lesson explains bipartite and complete bipartite graphs. Then common named graphs are defined. mathispower4u.com
From playlist Graph Theory (Discrete Math)
A Tight Bound for Hypergraph Regularity - Guy Moshkovitz
Computer Science/Discrete Mathematics Seminar I Topic: A Tight Bound for Hypergraph Regularity Speaker: Guy Moshkovitz Affiliation: Harvard University Date: Febuary 27, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Bipartite perfect matching is in quasi-NC - Fenner
Computer Science/Discrete Mathematics Seminar I Topic: Bipartite perfect matching is in quasi-NC Speaker: Stephen Fenner Date:Monday, February 8 We show that the bipartite perfect matching problem is in quasi 𝖭𝖢2quasi-NC2. That is, it has uniform circuits of quasi-polynomial size and O(
From playlist Mathematics

Dependent random choice - Jacob Fox
Marston Morse Lectures Topic: Dependent random choice Speaker: Jacob Fox, Stanford University Date: October 26, 2016 For more videos, visit http://video.ias.edu
From playlist Mathematics

PMSP - Quasi-random groups - Timothy Gowers
Timothy Gowers Cambridge University June 16, 2010 For more videos, visit http://video.ias.edu
From playlist Mathematics

A Regularity Lemma with Modifications - Guy Moshkovitz
Computer Science/Discrete Mathematics Seminar II Topic: A Regularity Lemma with Modifications Speaker: Guy Moshkovitz Affiliation: Member, School of Mathematics Date: January 29, 2019 For more video please visit http://video.ias.edu
From playlist Mathematics

Introduction to Matching in Bipartite Graphs (Hall's Marriage Theorem)
This video introduces matching in bipartite graphs. mathispower4u.com
From playlist Graph Theory (Discrete Math)

A glimpse of continuous combinatorics via natural quasirandomness - Leonardo Coregliano
Short Talks by Postdoctoral Members Topic: A glimpse of continuous combinatorics via natural quasirandomness Speaker: Leonardo Coregliano Affiliation: Member, School of Mathematics Date: September 23, 2021
From playlist Mathematics

13. Sparse regularity and the Green-Tao theorem
MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019 Instructor: Yufei Zhao View the complete course: https://ocw.mit.edu/18-217F19 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP62qauV_CpT1zKaGG_Vj5igX After discussion of Ramanujan graphs, Prof. Zhao discusse
From playlist MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019

Cedric Koh: Beyond value iteration for parity games: strategy iteration with universal trees
Parity games have witnessed several new quasi-polynomial algorithms since the breakthrough result of Calude et al. (2017). The central combinatorial object underlying these approaches is a universal tree, as identified by Czerwi´nski et al. (2019). By providing a quasi-polynomial lower bou
From playlist Workshop: Tropical geometry and the geometry of linear programming

Examples of non-positively curved groups - Kim Ruane
Women and Mathematics Title: Examples of non-positively curved groups Speaker: Kim Ruane Affiliation: Tufts University Date: May 23, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

14. Graph limits I: introduction
MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019 Instructor: Yufei Zhao View the complete course: https://ocw.mit.edu/18-217F19 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP62qauV_CpT1zKaGG_Vj5igX Graph limits provide a beautiful analytic framework for s
From playlist MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019