From playlist everything

Vodafone-Happy to Help Ad (full)
In some very special way I still remain loyal to this brand,yet another spectaculary meaningful ad from O&M..gd going
From playlist Advertisements

From playlist Music.

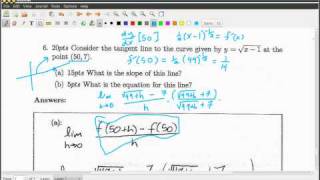
Is two the #antihero of the primes?
#math #antihero #manim #taylorswift #antiherochallenge #midnights @TaylorSwift
From playlist MathShorts

Stereolab - With Friends Like These
Stereolab - With Friends Like These
From playlist the absolute best of stereolab

Open educational video for the day
In today's video we take a look at an example of a product group https://www.youtube.com/watch?v=w2zo2sA1H2k
From playlist Fun!!!
https://www.math.ias.edu/files/media/agenda.pdf More videos on http://video.ias.edu
From playlist Mathematics

The Procrastination Killer: 5 Easy Steps To Get Things Done
Procrastination is super hard to get over. In this video I give you a step by step plan that you can follow that can help you defeat procrastination. Do you have any other advice? If so, please leave a comment below. Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear https://a
From playlist Inspiration and Advice

Parahoric Subgroups and Supercuspidal Representations of p-Adic groups - Dick Gross
Dick Gross Harvard University December 9, 2010 This is a report on some joint work with Mark Reeder and Jiu-Kang Yu. I will review the theory of parahoric subgroups and consider the induced representation of a one-dimensional character of the pro-unipotent radical. A surprising fact is th
From playlist Mathematics

Clark Barwick - 3/3 Exodromy for ℓ-adic Sheaves
In joint work with Saul Glasman and Peter Haine, we proved that the derived ∞-category of constructible ℓ-adic sheaves ’is’ the ∞-category of continuous functors from an explicitly defined 1-category to the ∞-category of perfect complexes over ℚℓ. In this series of talks, I want to offer s
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Provided to YouTube by Symphonic Distribution Anyway · Pompeya Real ℗ 2015 Have You No Shame Music Publishing - Administered by Sony/ATV Released on: 2015-05-05 Auto-generated by YouTube.
From playlist New Wave/Electro Pop/Indie Pop: 2009 - 2017 (original!)

Hausdorff dimensions in p-adic analytic groups by Anitha Thillaisundaram
PROGRAM GROUP ALGEBRAS, REPRESENTATIONS AND COMPUTATION ORGANIZERS: Gurmeet Kaur Bakshi, Manoj Kumar and Pooja Singla DATE: 14 October 2019 to 23 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Determining explicit algebraic structures of semisimple group algebras is a fund
From playlist Group Algebras, Representations And Computation

Galois theory: Infinite Galois extensions
This lecture is part of an online graduate course on Galois theory. We show how to extend Galois theory to infinite Galois extensions. The main difference is that the Galois group has a topology, and intermediate field extensions now correspond to closed subgroups of the Galois group. We
From playlist Galois theory

Coherent (phi, Gamma)-modules and cohomology of local systems by Kiran Kedlaya
PERFECTOID SPACES ORGANIZERS : Debargha Banerjee, Denis Benois, Chitrabhanu Chaudhuri and Narasimha Kumar Cheraku DATE & TIME : 09 September 2019 to 20 September 2019 VENUE : Madhava Lecture Hall, ICTS, Bangalore Scientific committee: Jacques Tilouine (University of Paris, France) Eknat
From playlist Perfectoid Spaces 2019

A Satake Isomorphism Mod.p - Guy Henniart
A Satake Isomorphism Mod.p Guy Henniart November 4, 2010 Let F be a locally compact non-Archimedean field, p its residue characteristic and G a connected reductive algebraic group over F . The classical Satake isomorphism describes the Hecke algebra (over the field of complex numbers) of
From playlist Mathematics

Lars Hesselholt: Around topological Hochschild homology (Lecture 7)
The lecture was held within the framework of the (Junior) Hausdorff Trimester Program Topology: "Workshop: Hermitian K-theory and trace methods" Introduced by Bökstedt in the late eighties, topological Hochschild homology is a manifestation of the dual visions of Connes and Waldhausen to
From playlist HIM Lectures: Junior Trimester Program "Topology"

Richard Hain: Mixed motives associated to elliptic curves
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

It's here! Vote vote vote! Everyone can vote! I desperately need votes! Free Music (Beginnings) from: http://music4yourvids.co.uk/
From playlist BAGUETTE

Richard Hain - 3/4 Universal mixed elliptic motives
Prof. Richard HAIN (Duke University, Durham, USA) Universal mixed elliptic motives are certain local systems over a modular curve that are endowed with additional structure, such as that of a variation of mixed Hodge structure. They form a tannakian category. The coordinate ring of its fu
From playlist Richard Hain - Universal mixed elliptic motives
