
Abstract Algebra | Principal Ideals of a Ring
We define the notion of a principal ideal of a ring and give some examples. We also prove that all ideals of the integers are principal ideals, that is, the integers form a principal ideal domain (PID). http://www.michael-penn.net https://www.researchgate.net/profile/Michael_Penn5 http://
From playlist Abstract Algebra

Ideals in Ring Theory (Abstract Algebra)
An ideal of a ring is the similar to a normal subgroup of a group. Using an ideal, you can partition a ring into cosets, and these cosets form a new ring - a "factor ring." (Also called a "quotient ring.") After reviewing normal subgroups, we will show you *why* the definition of an ide
From playlist Abstract Algebra
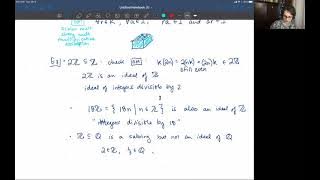
Principal Ideal Domains - Part I (Chapter 9)
From playlist Modern Algebra

RNT1.4. Ideals and Quotient Rings
Ring Theory: We define ideals in rings as an analogue of normal subgroups in group theory. We give a correspondence between (two-sided) ideals and kernels of homomorphisms using quotient rings. We also state the First Isomorphism Theorem for Rings and give examples.
From playlist Abstract Algebra

Rings 6 Prime and maximal ideals
This lecture is part of an online course on rings and modules. We discuss prime and maximal ideals of a (commutative) ring, use them to construct the spectrum of a ring, and give a few examples. For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj5
From playlist Rings and modules

RNT2.1. Maximal Ideals and Fields
Ring Theory: We now consider special types of rings. In this part, we define maximal ideals and explore their relation to fields. In addition, we note three ways to construct fields.
From playlist Abstract Algebra

Lecture 8. PIDs and Euclidean domains
From playlist Abstract Algebra 2

Ring Theory: As an application of all previous ideas on rings, we determine the primes in the Euclidean domain of Gaussian integers Z[i]. Not only is the answer somewhat elegant, but it contains a beautiful theorem on prime integers due to Fermat. We finish with examples of factorization
From playlist Abstract Algebra

[ANT04] Counting ideal classes
We don't always get unique factorisation. In those cases, can we measure how badly this uniqueness fails?
From playlist [ANT] An unorthodox introduction to algebraic number theory

Rings and modules 4 Unique factorization
This lecture is part of an online course on rings and modules. We discuss unique factorization in rings, showing the implications (Integers) implies (Euclidean domain) implies (Principal ideal domain) implies (Unique factorization domain). We give a few examples to illustrate these implic
From playlist Rings and modules

Abstract Algebra | Introduction to Principal Ideal Domains (PIDs)
After introducing the notion of a principal ideal domain (pid), we give some examples, and prove some simple results. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal Website: http://www.michael-penn.net Randolph College Math: http://www.randolphcolle
From playlist Abstract Algebra

Abstract Algebra | k[x] is a PID
We prove that every ideal of the polynomial ring k[x], where k is a field, is principal. That is, k[x] is a principal ideal domain. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal Website: http://www.michael-penn.net Randolph College Math: http://www
From playlist Abstract Algebra
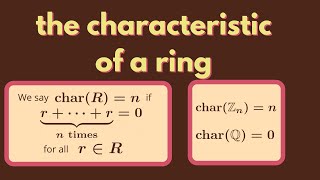
Abstract Algebra | The characteristic of a ring.
We define the characteristic of a ring and give some definitions. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Abstract Algebra | Ideals of quotients of PIDs
We prove that every ideal of a quotient of a principal ideal domain is also principal. Notice that the new space may not be an integral domain, so it is sometimes called a principal ring. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal Website: http:
From playlist Abstract Algebra

Commutative algebra 9 (Euclidean domains)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We describe one method of visualizing rings by drawing pictures of their points, and use this to show that the ring of Gaussia
From playlist Commutative algebra
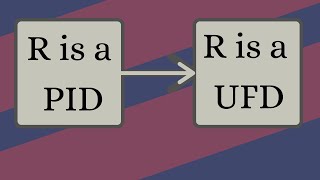
Abstract Algebra | Every PID is a UFD.
We prove the classical result in commutative algebra that every principal ideal domain is in fact a unique factorization domain. Along the way, we introduce the ascending chain condition and the notion of a Noetherian ring. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_co
From playlist Abstract Algebra

Schemes 39: Divisors and Dedekind domains
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. In this lecture we describe Weil and Cartier divisors for Dedekind domains, showing that they correspond to the two classical ways of defining the class group
From playlist Algebraic geometry II: Schemes

From playlist Abstract Algebra 2
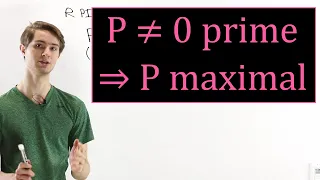
Proof: Prime Ideals are Maximal in a PID
In a principal ideal domain, if an ideal is a prime ideal, that implies it is a maximal ideal, as long as it is not just the zero ideal. Here we give a straightforward explanation of this theorem from ring theory! Ring & Module Theory playlist: https://www.youtube.com/playlist?list=PLug5Z
From playlist Ring & Module Theory