
What exactly is space? Brian Greene explains what the "stuff" around us is. Subscribe to our YouTube Channel for all the latest from World Science U. Visit our Website: http://www.worldscienceu.com/ Like us on Facebook: https://www.facebook.com/worldscienceu Follow us on Twitter: https:
From playlist Science Unplugged: Physics

Introduction to Angles (Precalculus - Trigonometry 1)
An introduction to Angles and their usage from standard position on the rectangular coordinate system. Support: https://www.patreon.com/ProfessorLeonard
From playlist Precalculus - College Algebra/Trigonometry

PreCalculus - Introduction/Preview of What is in this PreCalculus Series
Visit http://ilectureonline.com for more math and science lectures! In this video I will introduce and preview of the content of this Pre-Calculus series.
From playlist Michel van Biezen: PRECALCULUS 1-5 - ALGEBRA REVIEW

An Introduction to Trigonometric Functions
An introduction to trigonometry and trig functions. It's really important to have a strong foundation moving forward, so here are all the basics. Hopefully this video helps! Facebook: https://www.facebook.com/braingainzofficial Instagram: https://www.instagram.com/braingainzofficial T
From playlist Precalculus

Finding the Domain of Functions (Precalculus - College Algebra 4)
Support: https://www.patreon.com/ProfessorLeonard Cool Mathy Merch: https://professor-leonard.myshopify.com/ What the Domain means for functions, what to look for, and how to find it for basic functions.
From playlist Precalculus - College Algebra/Trigonometry

(January 28, 2013) Leonard Susskind presents three possible geometries of homogeneous space: flat, spherical, and hyperbolic, and develops the metric for these spatial geometries in spherical coordinates. Originally presented in the Stanford Continuing Studies Program. Stanford Universit
From playlist Lecture Collection | Cosmology

Pre-Calculus - Vocabulary of functions
This video describes some of the vocabulary used with functions. Specifically it covers what a function is as well as the basic idea behind its domain and range. For more videos visit http://www.mysecretmathtutor.com
From playlist Pre-Calculus - Functions

Trigonometric Functions and the Unit Circle (Precalculus - Trigonometry 6)
The creation of the Unit Circle and how it relates to Right Triangle Trigonometry and the creation of Trigonometric Functions. Support: https://www.patreon.com/ProfessorLeonard
From playlist Precalculus - College Algebra/Trigonometry

Basic Properties of Trigonometric Functions (Precalculus - Trigonometry 8)
A discovery of the basic properties of Trigonometric Functions and why they work. Also, a technique for using the period of Trig Functions to simplify angles more than 2pi. Support: https://www.patreon.com/ProfessorLeonard
From playlist Precalculus - College Algebra/Trigonometry

CGSR Seminar Series | War in Space: Strategy, Spacepower, Geopolitics
Speaker Biography Bleddyn Bowen primary research interests concern modern warfare, politics, and security in outer space, as well as classical strategic theory. Dr. Bowen provides research-led teaching in his 3rd year specialist module PL3144 Politics and War in Outer Space. He is the au
From playlist Center for Global Security Research

10. The Four Fundamental Subspaces
MIT 18.06 Linear Algebra, Spring 2005 Instructor: Gilbert Strang View the complete course: http://ocw.mit.edu/18-06S05 YouTube Playlist: https://www.youtube.com/playlist?list=PLE7DDD91010BC51F8 10. The Four Fundamental Subspaces License: Creative Commons BY-NC-SA More information at http
From playlist MIT 18.06 Linear Algebra, Spring 2005
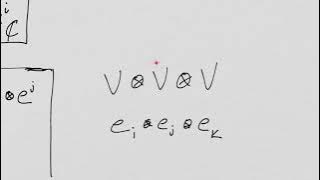
[Lesson 11] QED Prerequisites - Tensor Product Spaces
We take a detour from the Angular Momentum Mind Map to cover the important topic of Tensor Product spaces in the Dirac Formalism. In quantum mechanics, the notion of tensors is hidden under the hood of the formalism and this lesson opens that hood. The goal is to make us confident that we
From playlist QED- Prerequisite Topics

Nicolò Zava (3/17/23): Every stable invariant of finite metric spaces produces false positives
In computational topology and geometry, the Gromov-Hausdorff distance between metric spaces provides a theoretical framework to tackle the problem of shape recognition and comparison. However, the direct computation of the Gromov-Hausdorff distance between finite metric spaces is known to
From playlist Vietoris-Rips Seminar

CGSR Seminar Series | U.S. National Security Space Strategy: The Cold War to the Present
Talk Abstract At the present time, U.S. government officials are faced with the increasingly complex task of protecting critical national security space infrastructure in a rapidly evolving threat environment. When placed in a historical context, we find that anxiety about space security
From playlist Center for Global Security Research

Vice President Pence Calls for Human Missions to Moon, Mars at National Space Council
Vice President Mike Pence called for returning U.S. astronauts to the Moon and eventual missions to Mars during the first meeting of the National Space Council, held on October 5 at the Smithsonian National Air and Space Museum’s Steven F. Udvar-Hazy Center, outside Washington. Chaired by
From playlist Return to the Moon Playlist

Sanjay Mishra: Preservation of Properties during Topological Equivalence of Function Space
Sanjay Mishra, Lovely Professional University Title: Preservation of Properties during Topological Equivalence of Function Space The study of convergence of sequence of functions is the most important and active area of research in theoretical mathematics that solve several problems of app
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022

Marvels of Space-Time | Episode 705 | Closer To Truth
Einstein showed that space and time are essentially the same thing-a single entity, space-time. But space and time seem so radically different. How could space and time be literally the same thing? Featuring interviews with Max Tegmark, J. Gott, Juan Maldacena, Fotini Markopoulou, and Joh
From playlist Closer To Truth | Season 7

CS224W: Machine Learning with Graphs | 2021 | Lecture 19.2 - Hyperbolic Graph Embeddings
For more information about Stanford’s Artificial Intelligence professional and graduate programs, visit: https://stanford.io/3Brc7vN Jure Leskovec Computer Science, PhD In previous lectures, we focused on graph representation learning in Euclidean embedding spaces. In this lecture, we in
From playlist Stanford CS224W: Machine Learning with Graphs

What is (a) Space? From Zero to Geo 1.5
What is space? In this video, we learn about the many different things that we might call "space". We come up with both a geometric and an algebraic definition, and the discussion also leads us to the important concept of subspaces. Sorry for how long this video took to make! I mention
From playlist From Zero to Geo

What is a Tensor 13: Realization of a Vector Space
What is a Tensor 13: Realization of a Vector Space Note: There is an error at 3:26. The equality I write down is only true for orthonormal basis vectors! There will always be a relationship between (e_\mu, e_\nu) and (e^\mu , e^\nu) but it wont always be as simple as I wrote down! For som
From playlist What is a Tensor?