
👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties

David Meyer (1/30/18): Some algebraic stability theorems for generalized persistence modules
From an algebraic point of view, generalized persistence modules can be interpreted as finitely-generated modules for a poset algebra. We prove an algebraic analogue of the isometry theorem of Bauer and Lesnick for a large class of posets. This theorem shows that for such posets, the int
From playlist AATRN 2018

👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties

👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties

On Finite Types That Are Not h-Sets - Sergey Melikhov
Sergey Melikhov Steklov Mathematical Institute; Member, School of Mathematics February 14, 2013 For more videos, visit http://video.ias.edu
From playlist Mathematics

Model Theory - part 04 - Posets, Lattices, Heyting Algebras, Booleans Algebras
This is a short video for people who haven't seen a Heyting algebras before. There is really nothing special in it that doesn't show up in wikipedia or ncatlab. I just wanted to review it before we use them. Errata: *at 3:35: there the law should read (a and (a or b) ), not (a and (a and
From playlist Model Theory
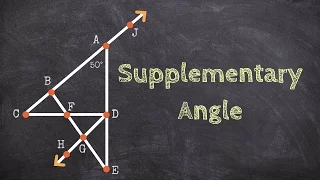
Determining two angles that are supplementary
👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships From a Figure
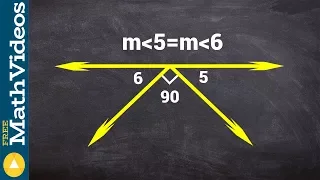
Determine the values of two angles that lie on a lie with a third angle
👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships From a Figure

Ulysses Alvarez - The Up Topology on the Grassmann Poset
38th Annual Geometric Topology Workshop (Online), June 15-17, 2021 Ulysses Alvarez, Binghamton University Title: The Up Topology on the Grassmann Poset Abstract: For a discrete poset X, McCord proved that there exists a weak homotopy equivalence from the order complex |X| to where X has
From playlist 38th Annual Geometric Topology Workshop (Online), June 15-17, 2021

What is an equilateral triangle
👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties

Kolja Knauer : Posets, polynômes, et polytopes - Partie 1
Résumé : Les posets (ensembles partiellement ordonnés) sont des structures utiles pour la modélisation de divers problèmes (scheduling, sous-groupes d'un groupe), mais ils sont aussi la base d'une théorie combinatoire très riche. Nous discuterons des paramètres de posets comme la largeur,
From playlist Combinatorics

Darij Grinberg - Noncommutative Birational Rowmotion on Rectangles
The operation of birational rowmotion on a finite poset has been a mainstay in dynamical algebraic combinatorics for the last 8 years. Since 2015, it is known that for a rectangular poset of the form [p]x[q], this operation is periodic with period p+q. (This result, as has been observed by
From playlist Combinatorics and Arithmetic for Physics: special days

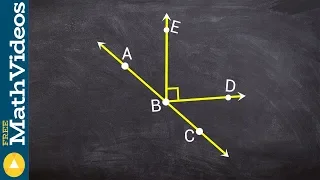
Determining if two angles are adjacent or not
👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships From a Figure

Serge Bouc: Correspondence functors
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties
Identify the type of angle from a figure acute, right, obtuse, straight ex 1
👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships
Sylvie PAYCHA - From Complementations on Lattices to Locality
A complementation proves useful to separate divergent terms from convergent terms. Hence the relevance of complementation in the context of renormalisation. The very notion of separation is furthermore related to that of locality. We extend the correspondence between Euclidean structures o
From playlist Algebraic Structures in Perturbative Quantum Field Theory: a conference in honour of Dirk Kreimer's 60th birthday

The Lawvere fixed point theorem
In this video we prove a version of Lawveres fixed point theorem that holds in Cartesian closed categories. It's a nice construction that specializes to results such as Cantors diagonal argument and prove the the power set of a set is classically always larger than the set itself. https:/
From playlist Logic
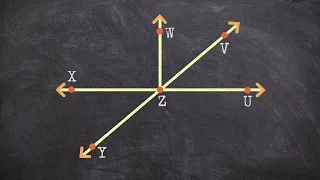
Determining if two angles are supplementary
👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships From a Figure

Steve Oudot (9/8/21): Signed barcodes for multi-parameter persistence via rank decompositions
In this talk I will introduce the signed barcode, a new visual representation of the global structure of the rank invariant of a multi-parameter persistence module or, more generally, of a poset representation. Like its unsigned counterpart in one-parameter persistence, the signed barcode
From playlist AATRN 2021