
Nomenclature of Polycyclic Compounds: Naphthalene, Biphenyl, Anthracene, Spiro, Bicyclo
We've done tons of IUPAC nomenclature for simple molecules, but once we start introducing multiple rings, things get trickier. This is especially the case because there are so many ways to get multiple rings. They can be fused, they can be bicyclic, aromatic or aliphatic, and every type ha
From playlist Organic Chemistry

What is Polypropylene and what is it used for?
From wiki: Polypropylene, also known as polypropene, is a thermoplastic polymer used in a wide variety of applications. It is produced via chain-growth polymerization from the monomer propylene. Polypropylene belongs to the group of polyolefins and is partially crystalline and non-polar. W
From playlist Materials Sciences 101 - Introduction to Materials Science & Engineering 2020

Polymorphs can be a headache for people who make pharmaceuticals. Find out why? More chemistry at http://www.periodicvideos.com/
From playlist Chem Definition - Periodic Videos

Professor Poliakoff on a word that sounds familiar. This is the first in our new Chem Definition series - short videos about the language and jargon of chemistry.
From playlist Chem Definition - Periodic Videos

Polynuclear Transition Metal Complexes
Up until now, all of the transition metal complexes we've been looking at have had a single metal center. But lots of these complexes can have more than one metal center. These are called polynuclear transition metal complexes. These metal centers may have bonds between them, or they may b
From playlist Inorganic/Organometallic Chemistry

Dihedral Group (Abstract Algebra)
The Dihedral Group is a classic finite group from abstract algebra. It is a non abelian groups (non commutative), and it is the group of symmetries of a regular polygon. This group is easy to work with computationally, and provides a great example of one connection between groups and geo
From playlist Abstract Algebra

What are four types of polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What is polycarbonate and what is it used for?
From wiki: Polycarbonates are a group of thermoplastic polymers containing carbonate groups in their chemical structures. Polycarbonates used in engineering are strong, tough materials, and some grades are optically transparent. They are easily worked, molded, and thermoformed. Wikipedia L
From playlist Materials Sciences 101 - Introduction to Materials Science & Engineering 2020

Bettina EICK - Computational group theory, cohomology of groups and topological methods 1
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to use them within GAP. Alexander Hulpke's lectures will being with some general computation
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Bettina EICK - Computational group theory, cohomology of groups and topological methods 2
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to use them within GAP. Alexander Hulpke's lectures will being with some general computation
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

p- groups - 1 by Heiko Dietrich
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

Bettina EICK - Computational group theory, cohomology of groups and topological methods 5
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to use them within GAP. Alexander Hulpke's lectures will being with some general computation
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

HSC Chemistry Organic Chemistry Polystyrene
From playlist Y12 Chem Mod 7 Organic Chem

Bettina EICK - Computational group theory, cohomology of groups and topological methods 4
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to use them within GAP. Alexander Hulpke's lectures will being with some general computation
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Bettina EICK - Computational group theory, cohomology of groups and topological methods 3
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to use them within GAP. Alexander Hulpke's lectures will being with some general computation
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Nexus Trimester - Delaram Kahrobaei (City University of New York)
Cryptosystems Based on Group-Theoretic Problems: A Survey, New Results, Open Problems Delaram Kahrobaei (City University of New York) March 31, 2016 Abstract: In this talk I will survey some of the cryptosystems based on group theoretic problems and their computational complexity such as
From playlist Nexus Trimester - 2016 - Secrecy and Privacy Theme

Alexander HULPKE - Computational group theory, cohomology of groups and topological methods 4
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to use them within GAP. Alexander Hulpke's lectures will being with some general computation
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Gilbert Levitt - Vertex finiteness for relatively hyperbolic groups
Gilbert Levitt (University of Caen, France) Given a finitely generated group G, we consider all splittings of G over subgroups in a fixed family (such as finite groups, cyclic groups, abelian groups). We discuss whether it is the case that only finitely many vertex groups appear, up to is
From playlist T1-2014 : Random walks and asymptopic geometry of groups.
Advice to Amateur Research Mathematicians: Poly Number theory-- future directions for greater import
Number theory is a very attractive subject, but in this video we argue that for prospective amateur researchers, the chance of making an important contribution is minimal. Better to focus on a much bigger and more wide open area: Poly Number theory! Polynumbers, developed in the Algebrai
From playlist Maxel inverses and orthogonal polynomials (non-Members)
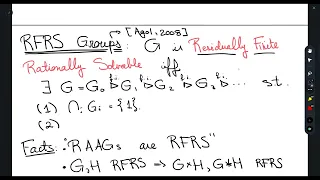
Sam Fisher: Fibring of RFRS groups
Sam Fisher, University of Oxford Title: Fibring of RFRS groups A group $G$ is said to algrebraically fibre if it admits an epimorphism to $\mathbb{Z}$ with finitely generated kernel. The motivation for this definition comes from a result of Stallings, which states that if $G$ is the fundam
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022