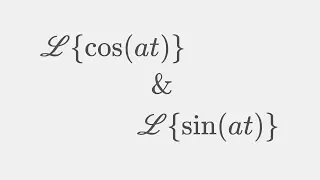
Laplace transform: sin(at) and cos(at)
Playlist: https://www.youtube.com/watchv=5RCijylGyK4&list=PLN2B6ZNu6xmfaT2IBigUylhfpFFA1L8Mp German version: https://youtu.be/ABX0kUx2WuM Update video: https://youtu.be/Hh6mR_vwWuw Let's, once again, kill two birds with one stone! We are taking a look at the laplace transformation of a ti
From playlist Laplace transform

Electrical Engineering: Ch 19: Fourier Transform (2 of 45) What is a Fourier Transform? Math Def
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain the mathematical definition and equation of a Fourier transform. Next video in this series can be seen at: https://youtu.be/yl6RtWp7y4k
From playlist ELECTRICAL ENGINEERING 18: THE FOURIER TRANSFORM

Animated Mandelbrot transform - linear interpolation
http://code.google.com/p/mandelstir/
From playlist mandelstir

Electrical Engineering: Ch 19: Fourier Transform (1 of 45) What is a Fourier Transform?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is a Fourier transform and how is it different from the Fourier series. Next video in this series can be seen at: https://youtu.be/fMHk6_1ZYEA
From playlist ELECTRICAL ENGINEERING 18: THE FOURIER TRANSFORM

Animated Mandelbrot Transform - linear interpolation, applied to an image of the Set itself
http://code.google.com/p/mandelstir/
From playlist mandelstir

The Fourier Transform and Derivatives
This video describes how the Fourier Transform can be used to accurately and efficiently compute derivatives, with implications for the numerical solution of differential equations. Book Website: http://databookuw.com Book PDF: http://databookuw.com/databook.pdf These lectures follow
From playlist Fourier

How to apply Fourier transforms to solve differential equations
Free ebook https://bookboon.com/en/partial-differential-equations-ebook How to apply Fourier transforms to solve differential equations. An example is discussed and solved.
From playlist Partial differential equations

Fourier transforms: heat equation
Free ebook https://bookboon.com/en/partial-differential-equations-ebook How to solve the heat equation via Fourier transforms. An example is discussed and solved.
From playlist Partial differential equations

C80 Solving a linear DE with Laplace transformations
Showing how to solve a linear differential equation by way of the Laplace and inverse Laplace transforms. The Laplace transform changes a linear differential equation into an algebraical equation that can be solved with ease. It remains to do the inverse Laplace transform to calculate th
From playlist Differential Equations

What Happens After the Universe Ends?
PBS Member Stations rely on viewers like you. To support your local station, go to: http://to.pbs.org/DonateSPACE ↓ More info below ↓ Sign Up on Patreon to get access to the Space Time Discord! https://www.patreon.com/pbsspacetime Check out the Space Time Merch Store https://pbsspacetim
From playlist The End of The Universe!

The Edge of an Infinite Universe
PBS Member Stations rely on viewers like you. To support your local station, go to: http://to.pbs.org/DonateSPACE ↓ More info below ↓ Have you ever asked “what is beyond the edge of the universe?” And have you ever been told that an infinite universe that has no edge? You were told wrong.
From playlist What Fraser's watching

Eigenvector and Eigenvalue Applications — Topic 34 of Machine Learning Foundations
In this video, I provide real-world applications of eigenvectors and eigenvalues, with special mention of applications that are directly relevant to machine learning. There are eight subjects covered comprehensively in the ML Foundations series and this video is from the second subject, "
From playlist Linear Algebra for Machine Learning

Oxford Mathematics Public Lectures : Roger Penrose - Eschermatics Roger Penrose's relationship with the artist M.C. Escher was not just one of mutual admiration. Roger's thinking was consistently influenced by Escher, from the famous Penrose tiling to his groundbreaking work in cosmology.
From playlist The Roger Penrose Playlist

Barak Weiss: Classification and statistics of cut-and-project sets
CIRM VIRTUAL CONFERENCE Recorded during the meeting " Diophantine Problems, Determinism and Randomness" the November 23, 2020 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide
From playlist Virtual Conference

Michael Eastwood: Twistor theory for LQG
Twistor Theory was proposed in the late 1960s by Roger Penrose as a potential geometric unification of general relativity and quantum mechanics. During the past 50 years, there have been many mathematical advances and achievements in twistor theory. In physics, however, there are aspirati
From playlist Mathematical Physics

Cup Products in Automorphic Cohomology - Matthew Kerr
Matthew Kerr Washington University in St. Louis March 30, 2012 In three very interesting and suggestive papers, H. Carayol introduced new aspects of complex geometry and Hodge theory into the study of non-classical automorphic representations -- in particular, those involving the totally d
From playlist Mathematics

What Happens at the Event Horizon? | Space Time | PBS Digital Studios
Viewers like you help make PBS (Thank you 😃) . Support your local PBS Member Station here: https://to.pbs.org/DonateSPACE What really happens when you approach the event horizon of a black hole? What do you see when you actually cross it? Matt shows you an elegant tool for understanding
From playlist Best of Space Time!

Lionel Mason (University of Oxford) - From Twistors to Gravitational Scattering (1/2)
This lecture will review how linear gravity can be obtained from integral formulae from twistor space and how the fully nonlinear self dual sector of 4d gravity can be built using complex analysis. It will focus on global problems in split signature where the self-dual sector can be genera
From playlist Balzan Lectures

Electrical Engineering: Ch 19: Fourier Transform (4 of 45) What is a Fourier Transform? Pulse Width
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain how the pulse width changes of a Fourier transform. Next video in this series can be seen at: https://youtu.be/QIb4_CagoH0
From playlist ELECTRICAL ENGINEERING 18: THE FOURIER TRANSFORM

Robert Fathauer - Tessellations: Mathematics, Art, and Recreation - CoM Apr 2021
A tessellation, also known as a tiling, is a collection of shapes (tiles) that fit together without gaps or overlaps. Tessellations are a topic of mathematics research as well as having many practical applications, the most obvious being the tiling of floors and other surfaces. There are n
From playlist Celebration of Mind 2021