
CCSS What is the difference between Acute, Obtuse, Right and Straight Angles
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

CCSS What is an angle bisector
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

What is an angle and it's parts
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

What is a Tensor? Lesson 39: All Possible Operations
What is a Tensor? Lesson 39: All Possible Operations I moved rather quickly through this material because it is not a critical "need to know" topic. However, it was more interesting than I expected it to be.
From playlist What is a Tensor?

What is a Tensor? Lesson 38: Visualization of Forms: Tacks and Sheaves. And Honeycombs.
What is a Tensor? Lesson 38: Visualization of Forms Part 2 Continuing to complete the "visualization" of the four different 3-dimensional vector spaces when dim(V)=3. Erratta: Note: When the coordinate system is expanded the density of things *gets numerically larger* and the area/volum
From playlist What is a Tensor?

Clark Barwick - 3/3 Exodromy for ℓ-adic Sheaves
In joint work with Saul Glasman and Peter Haine, we proved that the derived ∞-category of constructible ℓ-adic sheaves ’is’ the ∞-category of continuous functors from an explicitly defined 1-category to the ∞-category of perfect complexes over ℚℓ. In this series of talks, I want to offer s
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

Marc Levine: Refined enumerative geometry (Lecture 1)
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Marc Levine: Refined enumerative geometry Abstract: Lecture 1: Milnor-Witt sheaves, motivic homotopy theory and Chow-Witt groups We review the Hoplins-Morel construction of the Miln
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

algebraic geometry 35 More on blow ups
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It continues the discussion of blowing up in the previous video, with examples, of blowing up the real affine plane, blowing up an ideal, and regularizing a ration map fro
From playlist Algebraic geometry I: Varieties

👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships From a Figure

CCSS What are supplementary and complementary angles
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

Robert Ghrist (5/1/21): Laplacians and Network Sheaves
This talk will begin with a simple introduction to cellular sheaves as a generalized notion of a network of algebraic objects. With a little bit of geometry, one can often define a Laplacian for such sheaves. The resulting Hodge theory relates the geometry of the Laplacian to the algebraic
From playlist TDA: Tutte Institute & Western University - 2021

Schemes 48: The canonical sheaf
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. In this lecture we define the canonical sheaf, giev a survey of some applications (Riemann-Roch theorem, Serre duality, canonical embeddings, Kodaira dimensio
From playlist Algebraic geometry II: Schemes

Clark Barwick - 2/3 Exodromy for ℓ-adic Sheaves
In joint work with Saul Glasman and Peter Haine, we proved that the derived ∞-category of constructible ℓ-adic sheaves ’is’ the ∞-category of continuous functors from an explicitly defined 1-category to the ∞-category of perfect complexes over ℚℓ. In this series of talks, I want to offer s
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory
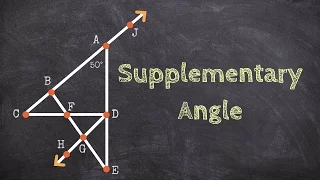
Determining two angles that are supplementary
👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships From a Figure
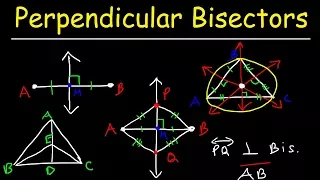
Perpendicular Bisector of a Line Segment and Triangle
This geometry video tutorial provides a basic introduction into the perpendicular bisector of a line segment and a triangle. it discusses the perpendicular bisector theorem and the definition of perpendicular bisectors in addition to how to use them in a geometry two column proof problem
From playlist Geometry Video Playlist
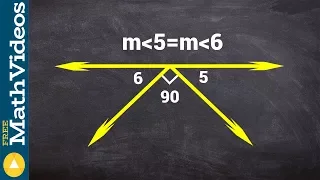
Determine the values of two angles that lie on a lie with a third angle
👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships From a Figure

Robert Ghrist (8/29/21): Laplacians and Network Sheaves
This talk will begin with a simple introduction to cellular sheaves as a generalized notion of a network of algebraic objects. With a little bit of geometry, one can often define a Laplacian for such sheaves. The resulting Hodge theory relates the geometry of the Laplacian to the algebraic
From playlist Beyond TDA - Persistent functions and its applications in data sciences, 2021

👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships
