
This video explains how to sketch vectors in R^3, how to determine the magnitude of a vector and how to determine a unit vector. http://mathispower4u.yolasite.com/
From playlist Vectors
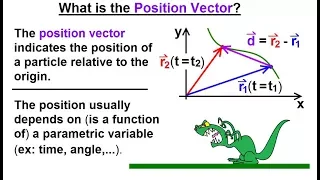
Calculus 3: Vector Calculus in 2D (17 of 39) What is the Position Vector?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is the position vector. The position vector indicates the position of a particle relative to the origin. The position usually depends on, or is a function of, a parametric variable (ex. t
From playlist CALCULUS 3 CH 3 VECTOR CALCULUS

Multivariable Calculus | The projection of a vector.
We define the projection of a vector in a certain direction. As an application we decompose a vector into the sum of a parallel and orthogonal component. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Vectors for Multivariable Calculus

Calculus 3: Vector Calculus in 2D (19 of 39) Position Vector Example
Visit http://ilectureonline.com for more math and science lectures! In this video I will find the position vector=? along a circle of radius r(t) where t=angle of the position vector. Next video in the series can be seen at: https://youtu.be/x2LhfDnNDxs
From playlist CALCULUS 3 CH 3 VECTOR CALCULUS

Angle Between a Line and a Plane (3 Examples)
I explain the geometry of find the angle between a line and a plane using a vector parallel to the line and a normal vector... perpendicular vector... to the plane, then work through 3 examples. Example 1) Find the angle between a line given in Cartesian form and a plane given in Cartes
From playlist Vector Math Lessons

How to compute the length and direction of a vector. Free ebook Free ebook https://bookboon.com/en/introduction-to-vectors-ebook (updated link) Test your understanding via a short quiz http://goo.gl/forms/0hPXc99Ql9
From playlist Introduction to Vectors

From playlist Linear Algebra Ch 6

The TRUTH about TENSORS, Part 9: Vector Bundles
In this video we define vector bundles in full abstraction, of which tangent bundles are a special case.
From playlist The TRUTH about TENSORS

This shows an small game that illustrates the concept of a vector. The clip is from the book "Immersive Linear Algebra" at http://www.immersivemath.com
From playlist Chapter 2 - Vectors

Index Theory, survey - Stephan Stolz [2018]
TaG survey series These are short series of lectures focusing on a topic in geometry and topology. May_8_2018 Stephan Stolz - Index Theory https://www3.nd.edu/~math/rtg/tag.html (audio fixed)
From playlist Mathematics
AMMI Course "Geometric Deep Learning" - Lecture 10 (Gauges) - Taco Cohen
Video recording of the course "Geometric Deep Learning" taught in the African Master in Machine Intelligence in July-August 2021 by Michael Bronstein (Imperial College/Twitter), Joan Bruna (NYU), Taco Cohen (Qualcomm), and Petar Veličković (DeepMind) Lecture 10: Gauges • Gauge transformat
From playlist AMMI Geometric Deep Learning Course - First Edition (2021)

PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics
From playlist Dualities in Topology and Algebra (Online)

Winter School JTP: Introduction to Fukaya categories, James Pascaleff, Lecture 1
This minicourse will provide an introduction to Fukaya categories. I will assume that participants are also attending Keller’s course on A∞ categories. Lecture 1: Basics of symplectic geometry for Fukaya categories. Symplectic manifolds; Lagrangian submanifolds; exactness conditions;
From playlist Winter School on “Connections between representation Winter School on “Connections between representation theory and geometry"

Luis Scoccola (5/3/21): Approximate and discrete vector bundles
Synchronization problems, such as the problem of reconstructing a 3D shape from a set of 2D projections, can often be modeled by principal bundles. Similarly, the application of local PCA to a point cloud concentrated around a manifold approximates the tangent bundle of the manifold. In th
From playlist TDA: Tutte Institute & Western University - 2021

Michael Farber (2/24/22): Topological complexity of spherical bundles
I will start by describing the concept of a parametrized motion planning algorithm which allows to achieve high degree of flexibility and universality. The main part of the talk will focus on the problem of understanding the parametrized topological complexity of sphere bundles. I will exp
From playlist Topological Complexity Seminar

Marc Levine - 1/3 Enumerative Geometry and Quadratic Forms
Notes: https://nextcloud.ihes.fr/index.php/s/BL5CJK4Ls8DT4S9 Enumerative Geometry and Quadratic Forms: Euler characteristics and Euler classes
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Orientations for Moduli Spaces in Higher-Dimensional Gauge Theory by Markus Upmeier
DISCUSSION MEETING ANALYTIC AND ALGEBRAIC GEOMETRY DATE:19 March 2018 to 24 March 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore. Complex analytic geometry is a very broad area of mathematics straddling differential geometry, algebraic geometry and analysis. Much of the interactions be
From playlist Analytic and Algebraic Geometry-2018

Hilbert Space Techniques in Complex Analysis and Geometry (Lecture 1) by Dror Varolin
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019

This video explains how to determine the projection of one vector onto another vector. http://mathispower4u.yolasite.com/
From playlist Vectors

Kirsten Wickelgren - Integrability Result for 𝔸^1-Euler Numbers
Notes: https://nextcloud.ihes.fr/index.php/s/q5f4YriEPGq6dBJ -- 𝔸^1-Euler numbers can be constructed with Hochschild homology, self-duality of Koszul complexes, pushforwards in 𝑆𝐿_𝑐 oriented cohomology theories, and sums of local degrees. We show an integrality result for 𝔸^1-Euler number
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory