Nonlinear conjugate gradient method

Gradient methods | Optimization algorithms and methods

In numerical optimization, the nonlinear conjugate gradient method generalizes the conjugate gradient method to nonlinear optimization. For a quadratic function the minimum of is obtained when the gradient is 0: . Whereas linear conjugate gradient seeks a solution to the linear equation , the nonlinear conjugate gradient method is generally used to find the local minimum of a nonlinear function using its gradient alone. It works when the function is approximately quadratic near the minimum, which is the case when the function is twice differentiable at the minimum and the second derivative is non-singular there. Given a function of variables to minimize, its gradient indicates the direction of maximum increase.One simply starts in the opposite (steepest descent) direction: with an adjustable step length and performs a line search in this direction until it reaches the minimum of : , After this first iteration in the steepest direction , the following steps constitute one iteration of moving along a subsequent conjugate direction , where : 1. * Calculate the steepest direction: , 2. * Compute according to one of the formulas below, 3. * Update the conjugate direction: 4. * Perform a line search: optimize , 5. * Update the position: , With a pure quadratic function the minimum is reached within N iterations (excepting roundoff error), but a non-quadratic function will make slower progress. Subsequent search directions lose conjugacy requiring the search direction to be reset to the steepest descent direction at least every N iterations, or sooner if progress stops. However, resetting every iteration turns the method into steepest descent. The algorithm stops when it finds the minimum, determined when no progress is made after a direction reset (i.e. in the steepest descent direction), or when some tolerance criterion is reached. Within a linear approximation, the parameters and are the same as in thelinear conjugate gradient method but have been obtained with line searches.The conjugate gradient method can follow narrow (ill-conditioned) valleys, where the steepest descent method slows down and follows a criss-cross pattern. Four of the best known formulas for are named after their developers: * Fletcher–Reeves: * Polak–Ribière: * Hestenes-Stiefel: * Dai–Yuan:. These formulas are equivalent for a quadratic function, but for nonlinear optimization the preferred formula is a matter of heuristics or taste. A popular choice is , which provides a direction reset automatically. Algorithms based on Newton's method potentially converge much faster. There, both step direction and length are computed from the gradient as the solution of a linear system of equations, with the coefficient matrix being the exact Hessian matrix (for Newton's method proper) or an estimate thereof (in the quasi-Newton methods, where the observed change in the gradient during the iterations is used to update the Hessian estimate). For high-dimensional problems, the exact computation of the Hessian is usually prohibitively expensive, and even its storage can be problematic, requiring memory (but see the limited-memory L-BFGS quasi-Newton method). The conjugate gradient method can also be derived using optimal control theory. In this accelerated optimization theory, the conjugate gradient method falls out as a nonlinear optimal feedback controller, for the double integrator system, The quantities and are variable feedback gains. (Wikipedia).

Introduction to the Gradient Theory and Formulas

Introduction to the Gradient Theory and Formulas If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Thank you:)

From playlist Calculus 3

The Gradient

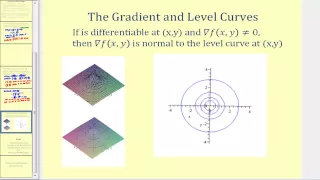
This video explains what information the gradient provides about a given function. http://mathispower4u.wordpress.com/

From playlist Functions of Several Variables - Calculus

11_3_1 The Gradient of a Multivariable Function

Using the partial derivatives of a multivariable function to construct its gradient vector.

From playlist Advanced Calculus / Multivariable Calculus

Find the Gradient Vector Field of f(x,y)=x^3y^5

This video explains how to find the gradient of a function. It also explains what the gradient tells us about the function. The gradient is also shown graphically. http://mathispower4u.com

From playlist The Chain Rule and Directional Derivatives, and the Gradient of Functions of Two Variables

Find the Gradient Vector Field of f(x,y)=ln(2x+5y)

This video explains how to find the gradient of a function. It also explains what the gradient tells us about the function. The gradient is also shown graphically. http://mathispower4u.com

From playlist The Chain Rule and Directional Derivatives, and the Gradient of Functions of Two Variables

Jorge Nocedal: "Tutorial on Optimization Methods for Machine Learning, Pt. 1"

Graduate Summer School 2012: Deep Learning, Feature Learning "Tutorial on Optimization Methods for Machine Learning, Pt. 1" Jorge Nocedal, Northwestern University Institute for Pure and Applied Mathematics, UCLA July 19, 2012 For more information: https://www.ipam.ucla.edu/programs/summ

From playlist GSS2012: Deep Learning, Feature Learning

Lecture 8.1 — A brief overview of Hessian-free optimization [Neural Networks for Machine Learning]

Lecture from the course Neural Networks for Machine Learning, as taught by Geoffrey Hinton (University of Toronto) on Coursera in 2012. Link to the course (login required): https://class.coursera.org/neuralnets-2012-001

From playlist [Coursera] Neural Networks for Machine Learning — Geoffrey Hinton

Approximating the Jacobian: Finite Difference Method for Systems of Nonlinear Equations

Generalized Finite Difference Method for Simultaneous Nonlinear Systems by approximating the Jacobian using the limit of partial derivatives with the forward finite difference. Example code on GitHub https://www.github.com/osveliz/numerical-veliz Chapters 0:00 Intro 0:13 Prerequisites 0:3

From playlist Solving Systems of Nonlinear Equations

Lecture 2.7 — Linear Regression With One Variable | Gradient Descent For Linear Regression

From playlist Machine Learning — Andrew Ng, Stanford University [FULL COURSE]

Directional Derivatives and the Gradient

From playlist Multivariable Calculus

11. Unconstrained Optimization; Newton-Raphson and Trust Region Methods

MIT 10.34 Numerical Methods Applied to Chemical Engineering, Fall 2015 View the complete course: http://ocw.mit.edu/10-34F15 Instructor: James Swan Students learned how to solve unconstrained optimization problems. In addition of the Newton-Raphson method, students also learned the steepe

From playlist MIT 10.34 Numerical Methods Applied to Chemical Engineering, Fall 2015

Optimization with inexact gradient and function by Serge Gratton

DISCUSSION MEETING : STATISTICAL PHYSICS OF MACHINE LEARNING ORGANIZERS : Chandan Dasgupta, Abhishek Dhar and Satya Majumdar DATE : 06 January 2020 to 10 January 2020 VENUE : Madhava Lecture Hall, ICTS Bangalore Machine learning techniques, especially “deep learning” using multilayer n

From playlist Statistical Physics of Machine Learning 2020

Lecture 8.1 — A brief overview of Hessian free optimization — [ Deep Learning | Hinton | UofT ]

From playlist Neural Networks for Machine Learning — Geoffrey Hinton, UofT [FULL COURSE]

Lecture 8A : A brief overview of "Hessian Free" optimization

Neural Networks for Machine Learning by Geoffrey Hinton [Coursera 2013] Lecture 8A : A brief overview of "Hessian Free" optimization

From playlist Neural Networks for Machine Learning by Professor Geoffrey Hinton [Complete]

Lecture 4.2 — Linear Regression With Multiple Variables -- (Gradient Descent For Multiple Variables)

From playlist Machine Learning — Andrew Ng, Stanford University [FULL COURSE]

Inverse problems for Maxwell's equations (Lecture - 1) by Ting Zhou

DISCUSSION MEETING WORKSHOP ON INVERSE PROBLEMS AND RELATED TOPICS (ONLINE) ORGANIZERS: Rakesh (University of Delaware, USA) and Venkateswaran P Krishnan (TIFR-CAM, India) DATE: 25 October 2021 to 29 October 2021 VENUE: Online This week-long program will consist of several lectures by

From playlist Workshop on Inverse Problems and Related Topics (Online)

Data assimilation and machine learning by Serge Gratton

From playlist Statistical Physics of Machine Learning 2020

Lecture 8/16 : More recurrent neural networks

Neural Networks for Machine Learning by Geoffrey Hinton [Coursera 2013] 8A A brief overview of "Hessian-Free" optimization 8B Modeling character strings with multiplicative connections 8C Learning to predict the next character using HF 8D Echo state networks

From playlist Neural Networks for Machine Learning by Professor Geoffrey Hinton [Complete]

Gradient

The gradient captures all the partial derivative information of a scalar-valued multivariable function.

From playlist Multivariable calculus

Graham Taylor: "Learning Representations of Sequences"

Graduate Summer School 2012: Deep Learning, Feature Learning "Learning Representations of Sequences" Graham Taylor, University of Guelph Institute for Pure and Applied Mathematics, UCLA July 13, 2012 For more information: https://www.ipam.ucla.edu/programs/summer-schools/graduate-summer

From playlist GSS2012: Deep Learning, Feature Learning

Nonlinear conjugate gradient method

Related pages