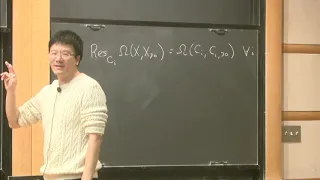Noncommutative algebraic varieties, their properties and geometric realizations II - Dmitry Orlov
Homological Mirror Symmetry Topic: Noncommutative algebraic varieties, their properties and geometric realizations II Speaker: Dmitry Orlov Affiliation: Mathematical Institute, Russian Academy of Sciences; Member, School of Mathematics Date: February 3, 2017 For more video, visit http:/
From playlist Mathematics

AlgTopReview4: Free abelian groups and non-commutative groups
Free abelian groups play an important role in algebraic topology. These are groups modelled on the additive group of integers Z, and their theory is analogous to the theory of vector spaces. We state the Fundamental Theorem of Finitely Generated Commutative Groups, which says that any such
From playlist Algebraic Topology

Noncommutative algebraic varieties, their properties... - Dmitry Orlov Steklov
Homological Mirror Symmetry (minicourse) Topic: Noncommutative algebraic varieties, their properties and geometric realizations Speaker: Dmitry Orlov Steklov Affiliation: Mathematical Institute, Russian Academy of Sciences; Member, School of Mathematics Date: February 1, 2017 For more vi
From playlist Mathematics

Noncommutative algebraic varieties, their properties and geometric realizations III - Dmitry Orlov
Topic: Noncommutative algebraic varieties, their properties and geometric realizations II Speaker: Dmitry Orlov Affiliation: Mathematical Institute, Russian Academy of Sciences; Member, School of Mathematics Date: February 8, 2017 For more video, visit http://video.ias.edu
From playlist Mathematics

Algebraic geometry 44: Survey of curves
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It gives an informal survey of complex curves of small genus.
From playlist Algebraic geometry I: Varieties

algebraic geometry 15 Projective space
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It introduces projective space and describes the synthetic and analytic approaches to projective geometry
From playlist Algebraic geometry I: Varieties

Sergey Shadrin: Arnold's trinity of algebraic 2d gravitation theories
Talk at the conference "Noncommutative geometry meets topological recursion", August 2021, University of Münster. Abstract: “Arnold’s trinities” refers to a metamathematical observation of Vladimir Arnold that many interesting mathematical concepts and theories occur in triples, with some
From playlist Noncommutative geometry meets topological recursion 2021

Andrzej Sitarz: Spectral action for 3+1 geometries
I'll demonstrate a class of models, to illustrate a principle of evolution for 3-dimensional noncommutative geometries, determined exclusively by a spectral action. One particular case is a model, which allows evolution of noncommutativeness (deformation parameter) itself for a specific c
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"
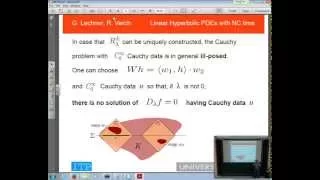
Rainer Verch: Linear hyperbolic PDEs with non-commutative time
Motivated by wave or Dirac equations on noncommutative deformations of Minkowski space, linear integro-differential equations of the form (D + sW) f = 0 are studied, where D is a normal or prenormal hyperbolic differential operator on Minkowski spacetime, s is a coupling constant, and W i
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Ben Webster - Representation theory of symplectic singularities
Research lecture at the Worldwide Center of Mathematics
From playlist Center of Math Research: the Worldwide Lecture Seminar Series

Anton Savin: Index problem for elliptic operators associated with group actions and ncg
Given a group action on a manifold, there is an associated class of operators represented as linear combinations of differential operators and shift operators along the orbits. Operators of this form appear in noncommutative geometry and mathematical physics when describing nonlocal phenom
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Franz Luef: Noncommutative geometry and time-frequency analysis
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist 30 years of wavelets

Piotr M. Hajac: Braided noncommutative join construction
We construct the join of noncommutative Galois objects (quantum torsors) over a Hopf algebra H. To ensure that the join algebra enjoys the natural (diagonal) coaction of H, we braid the tensor product of the Galois objects. Then we show that this coaction is principal. Our examples are bui
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Joachim Zacharias: Noncommutative covering dimension for C*-algebras and dynamical systems
(in collaboration with Hirshberg, Szabo, Winter, Wu) Various noncommutative generalisations of dimension have been considered and studies in the past decades. In recent years certain new dimension concepts for noncommutative C*-algebras, called nuclear dimension and a related dimension co
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Dmytro Shklyarov: Semi-infinite Hodge structures in noncommutative geometry
Abstract: Homological mirror symmetry asserts that the connection, discovered by physicists, between a count of rational curves in a Calabi-Yau manifold and period integrals of its mirror should follow from an equivalence between the derived Fukaya category of the first manifold and the de
From playlist Algebraic and Complex Geometry

Roberta Iseppi: The BV-BRST cohomology for U(n)-gauge theories induced by finitespectral triples
Talk at the conference "Noncommutative geometry meets topological recursion", August 2021, University of Münster. Abstract: The Batalin–Vilkovisky (BV) formalism provides a cohomological approach for the study of gauge symmetries: given a gauge theory, by introducing extra (non-existing) f
From playlist Noncommutative geometry meets topological recursion 2021

Complex surfaces 2: Minimal surfaces
This talk is part of a series about complex surfaces, and explains what minimal surfaces are. A minimial surfaces is one that cannot be obtained by blowing up a nonsingular surfaces at a point. We explain why every surface is birational to a minimal nonsingular projective surface. We disc
From playlist Algebraic geometry: extra topics

Snigdhayan Mahanta: Bivariant homology theories for noncommutative spaces
Familiar examples of bivariant homology theories include KK-theory and local cyclic homology. There is another one called noncommutative stable homotopy that is a universal example is a certain sense. They are defined on the category of noncommutative pointed compact spaces (or C*-algebras
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"