
Multimeter Review / DMM Review / buyers guide / tutorial
A list of my multimeters can be purchased here: http://astore.amazon.com/m0711-20?_encoding=UTF8&node=5 In this video I do a review of several digital multimeters. I compare features and functionality. I explain safety features, number of digits, display count, accuracy and resolution. Th
From playlist Multimeter reviews, buyers guide and comparisons.

Download the free PDF from http://tinyurl.com/EngMathYT This video shows how to apply the method of Lagrange multipliers to a max/min problem. Such ideas are seen in university mathematics.
From playlist Lagrange multipliers

Multivariable maxima and minima
A description of maxima and minima of multivariable functions, what they look like, and a little bit about how to find them.
From playlist Multivariable calculus

Multivariable Calculus | Differentiability
We give the definition of differentiability for a multivariable function and provide a few examples. http://www.michael-penn.net https://www.researchgate.net/profile/Michael_Penn5 http://www.randolphcollege.edu/mathematics/
From playlist Multivariable Calculus
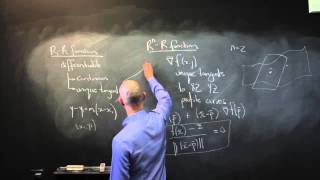
11_3_6 Continuity and Differentiablility
Prerequisites for continuity. What criteria need to be fulfilled to call a multivariable function continuous.
From playlist Advanced Calculus / Multivariable Calculus

Solving an equation with variables on both side and one solution
👉 Learn how to solve multi-step equations with variable on both sides of the equation. An equation is a statement stating that two values are equal. A multi-step equation is an equation which can be solved by applying multiple steps of operations to get to the solution. To solve a multi-s
From playlist Solve Multi-Step Equations......Help!
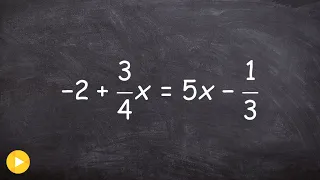
Solve an equation for x by clearing fractions with multiple steps
👉 Learn how to solve multi-step equations with variable on both sides of the equation. An equation is a statement stating that two values are equal. A multi-step equation is an equation which can be solved by applying multiple steps of operations to get to the solution. To solve a multi-s
From playlist How to Solve Multi Step Equations with Variables on Both Sides

Solving an equation with infinite many solutions 2a+3=3+2a
👉 Learn how to solve multi-step equations with variable on both sides of the equation. An equation is a statement stating that two values are equal. A multi-step equation is an equation which can be solved by applying multiple steps of operations to get to the solution. To solve a multi-s
From playlist How to Solve Multi Step Equations with Variables on Both Sides

Solving a multi-step equation with fractions and variable on both sides
👉 Learn how to solve multi-step equations with variable on both sides of the equation. An equation is a statement stating that two values are equal. A multi-step equation is an equation which can be solved by applying multiple steps of operations to get to the solution. To solve a multi-s
From playlist How to Solve Multi Step Equations with Variables on Both Sides

[ANT04] Counting ideal classes
We don't always get unique factorisation. In those cases, can we measure how badly this uniqueness fails?
From playlist [ANT] An unorthodox introduction to algebraic number theory

Visual Group Theory, Lecture 7.2: Ideals, quotient rings, and finite fields
Visual Group Theory, Lecture 7.2: Ideals, quotient rings, and finite fields A left (resp., right) ideal of a ring R is a subring that is invariant under left (resp., right) multiplication. Two-sided ideals are those that are both left and right ideals. This is the analogue of normal subgr
From playlist Visual Group Theory

R. Lazarsfeld: The Equations Defining Projective Varieties. Part 2
The lecture was held within the framework of the Junior Hausdorff Trimester Program Algebraic Geometry. (9.1.2014)
From playlist HIM Lectures: Junior Trimester Program "Algebraic Geometry"

Nonlinear algebra, Lecture 5: "Nullstellensätze ", by Bernd Sturmfels
This is the fifth lecture in the IMPRS Ringvorlesung, the advanced graduate course at the Max Planck Institute for Mathematics in the Sciences. Hilbert’s Nullstellensatz is a classical result from 1890, which offers a characterization of the set of all polynomials that vanish on a given v
From playlist IMPRS Ringvorlesung - Introduction to Nonlinear Algebra

I will discuss certain invariants of singularities, the Hodge ideals, that are defined in the context of Saito’s theory of mixed Hodge modules. They can be considered as higher order analogues of the multiplier ideals, invariants that have had a lot of applications in complex geometry. I w
From playlist Complex analytic and differential geometry - a conference in honor of Jean-Pierre Demailly - 6-9 juin 2017
Principal Ideal Domains - Part I (Chapter 9)
From playlist Modern Algebra

From playlist Abstract Algebra 2

Nonlinear algebra, Lecture 12: "Primary Decomposition ", by Mateusz Michalek and Bernd Sturmfels
This is the twelth lecture in the IMPRS Ringvorlesung, the advanced graduate course at the Max Planck Institute for Mathematics in the Sciences.
From playlist IMPRS Ringvorlesung - Introduction to Nonlinear Algebra

Ideals in Ring Theory (Abstract Algebra)
An ideal of a ring is the similar to a normal subgroup of a group. Using an ideal, you can partition a ring into cosets, and these cosets form a new ring - a "factor ring." (Also called a "quotient ring.") After reviewing normal subgroups, we will show you *why* the definition of an ide
From playlist Abstract Algebra

[ANT03] Ideal factorisation: recovering uniqueness
Last video, we saw an example of non-unique factorisation. In this video, we see how we might try to fix that, how it might help us, and what questions it raises.
From playlist [ANT] An unorthodox introduction to algebraic number theory
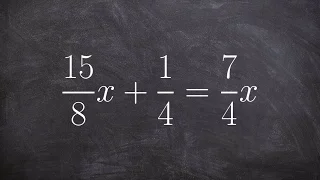
Solving an equation with fraction where your variable is on both sides
👉 Learn how to solve multi-step equations with variable on both sides of the equation. An equation is a statement stating that two values are equal. A multi-step equation is an equation which can be solved by applying multiple steps of operations to get to the solution. To solve a multi-s
From playlist How to Solve Multi Step Equations with Variables on Both Sides