
The Most Powerful Tool Based Entirely On Randomness
We see the effects of randomness all around us on a day to day basis. In this video we’ll be discussing a couple of different techniques that scientists use to understand randomness, as well as how we can harness its power. Basically, we'll study the mathematics of randomness. The branch
From playlist Classical Physics by Parth G

(PP 6.7) Geometric intuition for the multivariate Gaussian (part 2)
How to visualize the effect of the eigenvalues (scaling), eigenvectors (rotation), and mean vector (shift) on the density of a multivariate Gaussian.
From playlist Probability Theory
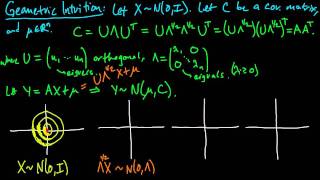
(PP 6.6) Geometric intuition for the multivariate Gaussian (part 1)
How to visualize the effect of the eigenvalues (scaling), eigenvectors (rotation), and mean vector (shift) on the density of a multivariate Gaussian.
From playlist Probability Theory

Probabilities involving Equally Likely Outcomes | Probability Theory
How do we assess probabilities of events in sample spaces that have equal outcomes? Like tossing a coin or a die? We'll be going over some of these basic probability concepts in today's probability theory lesson! We'll also touch on an example of the inclusion exclusion principle for proba
From playlist Probability Theory

Francesco Mezzadri: Moments of Random Matrices and Hypergeometric Orthogonal Polynomials
We establish a new connection between moments of n×n random matrices $X_{n}$ and hypergeometric orthogonal polynomials. Specifically, we consider moments $\mathbb{E}\mathrm{Tr} X_n^{-s}$ as a function of the complex variable $s\in\mathbb{C}$, whose analytic structure we describe completely
From playlist Jean-Morlet Chair - Grava/Bufetov

(PP 6.1) Multivariate Gaussian - definition
Introduction to the multivariate Gaussian (or multivariate Normal) distribution.
From playlist Probability Theory

(PP 4.5) Mean, variance, and moments
Definitions of mean, variance, and moments. A playlist of the Probability Primer series is available here: http://www.youtube.com/view_play_list?p=17567A1A3F5DB5E4
From playlist Probability Theory

(PP 6.3) Gaussian coordinates does not imply (multivariate) Gaussian
An example illustrating the fact that a vector of Gaussian random variables is not necessarily (multivariate) Gaussian.
From playlist Probability Theory

Ex: Determine Conditional Probability from a Table
This video provides two examples of how to determine conditional probability using information given in a table.
From playlist Probability

Persi Diaconis: Haar-distributed random matrices - in memory of Elizabeth Meckes
Elizabeth Meckes spent many years studying properties of Haar measure on the classical compact groups along with applications to high dimensional geometry. I will review some of her work and some recent results I wish I could have talked about with her.
From playlist Winter School on the Interplay between High-Dimensional Geometry and Probability

Rafał Kulik: Blocks estimators in Extreme Value Theory
Rafał Kulik, University of Ottawa 10 November 2022 Abstract: Extreme value theory deals with large values and rare events. These large values tend to cluster in case of temporal dependence. This clustering behaviour is widely observed in practice. I will start with a mild introduction to
From playlist SMRI Seminars

Tom Claeys: Optimal global rigidity estimates in unitary invariant ensembles
A fundamental question in random matrix theory is to understand how much the eigenvalues of a random matrix fluctuate. I will address this question in the context of unitary invariant ensembles, by studying the global rigidity of the eigenvalues, or in other words the maximal deviation of
From playlist Probability and Statistics

Absolute continuity of limiting spectral distributions of Toeplitz... by Manjunath Krishnapur
PROGRAM: ADVANCES IN APPLIED PROBABILITY ORGANIZERS: Vivek Borkar, Sandeep Juneja, Kavita Ramanan, Devavrat Shah, and Piyush Srivastava DATE & TIME: 05 August 2019 to 17 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Applied probability has seen a revolutionary growth in resear
From playlist Advances in Applied Probability 2019

Infinite-density versus large deviations theory for fat-tailed systems by Erez Aghion
Large deviation theory in statistical physics: Recent advances and future challenges DATE: 14 August 2017 to 13 October 2017 VENUE: Madhava Lecture Hall, ICTS, Bengaluru Large deviation theory made its way into statistical physics as a mathematical framework for studying equilibrium syst
From playlist Large deviation theory in statistical physics: Recent advances and future challenges

Shi Jin: Asymptotic preserving methods for multi-scale physical problems - lecture 1
We will first outline the asymptotic-transition from quantum to classical, to kinetic and then the hydrodynamic equations, and then show how such asymptotics can guide the design and analysis of the so-called asymptotic-preserving schemes that offer efficient multiscale computations betwee
From playlist Virtual Conference

How Do We Know What We Know? Philosophy of Science
What's the backbone behind all our scientific knowledge? How can we improve our methodologies and understand our world better? These are the kind of questions that the Philosophy of Science deals with. We're discussing how these things fit in the modern world of science with Professor Sam
From playlist Interviews

The subconvexity problem for L-functions – Ritabrata Munshi – ICM2018
Number Theory Invited Lecture 3.7 The subconvexity problem for L-functions Ritabrata Munshi Abstract: Estimating the size of automorphic L-functions on the critical line is a central problem in analytic number theory. An easy consequence of the standard analytic properties of the L-funct
From playlist Number Theory

Josephine Evans: Using Harris’s theorem to show convergence to equilibrium for kinetic equations
Abstract: I will discuss a joint work with Jose Canizo, Cao Chuqi and Havva Yolda. I will introduce Harris’s theorem which is a classical theorem from the study of Markov Processes. Then I will discuss how to use this to show convergence to equilibrium for some spatially inhomogeneous kine
From playlist Probability and Statistics

(PP 6.2) Multivariate Gaussian - examples and independence
Degenerate multivariate Gaussians. Some sketches of examples and non-examples of Gaussians. The components of a Gaussian are independent if and only if they are uncorrelated.
From playlist Probability Theory

3 Nandakumaran - An Introduction to deterministic optimal control and controllability
PROGRAM NAME :WINTER SCHOOL ON STOCHASTIC ANALYSIS AND CONTROL OF FLUID FLOW DATES Monday 03 Dec, 2012 - Thursday 20 Dec, 2012 VENUE School of Mathematics, Indian Institute of Science Education and Research, Thiruvananthapuram Stochastic analysis and control of fluid flow problems have
From playlist Winter School on Stochastic Analysis and Control of Fluid Flow