
Coefficient of Variation Example and Explanation
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Coefficient of Variation Example and Explanation.
From playlist Statistics

Statistics - How to calculate the coefficient of variation
In this video I'll quickly show you how to find the coefficient of variation. There are two formulas for samples and populations, but these are basically the same and involve dividing the standard deviation by the mean and lastly converting to a percent. The coefficient of variation is u
From playlist Statistics

Free ebook http://tinyurl.com/EngMathYT I show how to solve differential equations by applying the method of variation of parameters for those wanting to review their understanding.
From playlist Differential equations
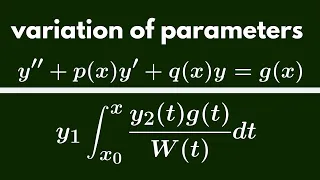
Differential Equations | Variation of Parameters.
We derive the general form for a solution to a differential equation using variation of parameters. http://www.michael-penn.net
From playlist Differential Equations

Asymptotic enumeration of graphs with given degree sequence – Nicholas Wormald – ICM2018
Combinatorics Invited Lecture 13.7 Asymptotic enumeration of graphs with given degree sequence Nicholas Wormald Abstract: We survey results on counting graphs with given degree sequence, focusing on asymptotic results, and mentioning some of the applications of these results. The main re
From playlist Combinatorics

C34 Expanding this method to higher order linear differential equations
I this video I expand the method of the variation of parameters to higher-order (higher than two), linear ODE's.
From playlist Differential Equations

Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Measures of Variation
From playlist Statistics

Lecture 13/16 : Stacking RBMs to make Deep Belief Nets
Neural Networks for Machine Learning by Geoffrey Hinton [Coursera 2013] 13A The ups and downs of backpropagation 13B Belief Nets 13C Learning Sigmoid Belief Nets 13D The wake-sleep algorithm
From playlist Neural Networks for Machine Learning by Professor Geoffrey Hinton [Complete]

Differential Equations | Variation of Parameters Example 1
We solve a second order linear differential equation using the method of variation of parameters.
From playlist Differential Equations

Differential Equations | Variation of Parameters Example 2
We solve a second order linear differential equation using the method of variation of parameters.
From playlist Differential Equations

AQC 2016 - Controlled Interactions Between Superconducting Qubits for Adiabatic Quantum Simulations
A Google TechTalk, June 28, 2016, presented by Stefan Filipp (IBM Research) ABSTRACT: The controlled realization of different types of interactions between qubits without compromising their coherence is essential for adiabatic and analog quantum simulations. In the context of superconduct
From playlist Adiabatic Quantum Computing Conference 2016

CSDM: Finding Needles in Exponential Haystacks - Joel Spencer
Joel Spencer Courant Institute, NYU February 21, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics
ML Tutorial: Gaussian Processes (Richard Turner)
Machine Learning Tutorial at Imperial College London: Gaussian Processes Richard Turner (University of Cambridge) November 23, 2016
From playlist Machine Learning Tutorials

Variation of Parameters y'' + y = sin^2(x)
Variation of Parameters y'' + y = sin^2(x) If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Thank you:)
From playlist Zill DE 4.6 Variation of Parameters

Lie Fu: Multiplicative McKay correspondence for surfaces
30 September 2021 Abstract: Given a nite subgroup of SL(2,C), the classical 2-dimensional McKay correspondence provides a connection between the representation theory of the group and the exceptional divisor of the minimal resolution of the quotient singularity that the group naturally gi
From playlist Representation theory's hidden motives (SMRI & Uni of Münster)

Q&A - New Discoveries in Population Genetics - with Enrico Coen
Can fitness landscapes be measured? How aggressively do populations invade other niches? Enrico Coen answers questions from the audience following his talk. Subscribe for regular science videos: http://bit.ly/RiSubscRibe Watch the full talk here: https://youtu.be/Q4QS62qMImw This Q&A and
From playlist Ri Talks

Ender Konukoglu: "On Bayesian models with networks for reconstruction and detection"
Deep Learning and Medical Applications 2020 "On Bayesian models with networks for reconstruction and detection" Ender Konukoglu, ETH Zurich Abstract: Neural networks have demonstrated tremendous potential for medical image analysis. In this talk, I will focus on utilizing these models in
From playlist Deep Learning and Medical Applications 2020

Moduli of Representations and Pseudorepresentations - Carl Wang Erickson
Carl Wang Erickson Harvard University May 2, 2013 A continuous representation of a profinite group induces a continuous pseudorepresentation, where a pseudorepresentation is the data of the characteristic polynomial coefficients. We discuss the geometry of the resulting map from the moduli
From playlist Mathematics

Numerical Homogenization by Localized Orthogonal Decomposition (Lecture 1) by Daniel Peterseim
DISCUSSION MEETING Multi-Scale Analysis: Thematic Lectures and Meeting (MATHLEC-2021, ONLINE) ORGANIZERS: Patrizia Donato (University of Rouen Normandie, France), Antonio Gaudiello (Università degli Studi di Napoli Federico II, Italy), Editha Jose (University of the Philippines Los Baño
From playlist Multi-scale Analysis: Thematic Lectures And Meeting (MATHLEC-2021) (ONLINE)

Variation of parameters to solve differential equations
Free ebook http://tinyurl.com/EngMathYT How to use the method of variation of parameters to solve second order ordinary differential equations with constant coefficients. Several examples are discussed.
From playlist Differential equations