
This video defines a cylindrical surface and explains how to graph a cylindrical surface. http://mathispower4u.yolasite.com/
From playlist Quadric, Surfaces, Cylindrical Coordinates and Spherical Coordinates

MATH331: Riemann Surfaces - part 1
We define what a Riemann Surface is. We show that PP^1 is a Riemann surface an then interpret our crazy looking conditions from a previous video about "holomorphicity at infinity" as coming from the definition of a Riemann Surface.
From playlist The Riemann Sphere

L. Mazet - Minimal hypersurfaces of least area
In this talk, I will present a joint work with H. Rosenberg where we give a characterization of the minimal hypersurface of least area in any Riemannian manifold. As a consequence, we give a lower bound for the area of a minimal surface in a hyperbolic 3-manifold.
From playlist Ecole d'été 2016 - Analyse géométrique, géométrie des espaces métriques et topologie
From playlist Surface integrals
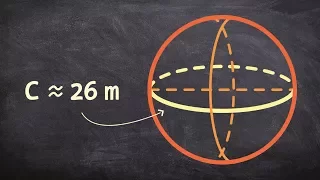
Find the volume of a sphere given the circumference
👉 Learn how to find the volume and the surface area of a sphere. A sphere is a perfectly round 3-dimensional object. It is an object with the shape of a round ball. The distance from the center of a sphere to any point on its surface is called the radius of the sphere. A sphere has a unifo
From playlist Volume and Surface Area
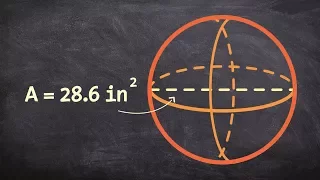
Learn how to determine the volume of a sphere
👉 Learn how to find the volume and the surface area of a sphere. A sphere is a perfectly round 3-dimensional object. It is an object with the shape of a round ball. The distance from the center of a sphere to any point on its surface is called the radius of the sphere. A sphere has a unifo
From playlist Volume and Surface Area

Surface Area of Prisms and Pyramids
This video is about finding the Surface Area of Prisms and Pyramids
From playlist Surface Area and Volume

Finding the volume and the surface area of a sphere
👉 Learn how to find the volume and the surface area of a sphere. A sphere is a perfectly round 3-dimensional object. It is an object with the shape of a round ball. The distance from the center of a sphere to any point on its surface is called the radius of the sphere. A sphere has a unifo
From playlist Volume and Surface Area

How do you find the surface area of a sphere
👉 Learn how to find the volume and the surface area of a sphere. A sphere is a perfectly round 3-dimensional object. It is an object with the shape of a round ball. The distance from the center of a sphere to any point on its surface is called the radius of the sphere. A sphere has a unifo
From playlist Volume and Surface Area

Zero mean curvature surfaces in Euclidean and Lorentz-Minkowski....(Lecture 3) by Shoichi Fujimori
Discussion Meeting Discussion meeting on zero mean curvature surfaces (ONLINE) Organizers: C. S. Aravinda and Rukmini Dey Date: 07 July 2020 to 15 July 2020 Venue: Online Due to the ongoing COVID-19 pandemic, the original program has been canceled. However, the meeting will be conduc
From playlist Discussion Meeting on Zero Mean Curvature Surfaces (Online)

Embeddedness of timelike maximal surfaces in (1+2) Minkowski Space by Edmund Adam Paxton
Discussion Meeting Discussion meeting on zero mean curvature surfaces (ONLINE) Organizers: C. S. Aravinda and Rukmini Dey Date: 07 July 2020 to 15 July 2020 Venue: Online Due to the ongoing COVID-19 pandemic, the original program has been canceled. However, the meeting will be co
From playlist Discussion Meeting on Zero Mean Curvature Surfaces (Online)

Zero mean curvature surfaces in Euclidean and Lorentz-Minkowski....(Lecture 2) by Shoichi Fujimori
Discussion Meeting Discussion meeting on zero mean curvature surfaces (ONLINE) Organizers: C. S. Aravinda and Rukmini Dey Date: 07 July 2020 to 15 July 2020 Venue: Online Due to the ongoing COVID-19 pandemic, the original program has been canceled. However, the meeting will be conduc
From playlist Discussion Meeting on Zero Mean Curvature Surfaces (Online)

Minimal surfaces in R^3 and Maximal surfaces in L^3 (Lecture 3) by Pradip Kumar
ORGANIZERS : C. S. Aravinda and Rukmini Dey DATE & TIME : 16 June 2018 to 25 June 2018 VENUE : Madhava Lecture Hall, ICTS, Bangalore This workshop on geometry and topology for lecturers is aimed for participants who are lecturers in universities/institutes and colleges in India. This w
From playlist Geometry and Topology for Lecturers

D. Stern - Harmonic map methods in spectral geometry (version temporaire)
Over the last fifty years, the problem of finding sharp upper bounds for area-normalized Laplacian eigenvalues on closed surfaces has attracted the attention of many geometers, due in part to connections to the study of sphere-valued harmonic maps and minimal immersions. In this talk, I'll
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

D. Stern - Harmonic map methods in spectral geometry
Over the last fifty years, the problem of finding sharp upper bounds for area-normalized Laplacian eigenvalues on closed surfaces has attracted the attention of many geometers, due in part to connections to the study of sphere-valued harmonic maps and minimal immersions. In this talk, I'll
From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Entanglement Relations and Bulk Locality by Veronika Hubeny
ORGANIZERS : Pallab Basu, Avinash Dhar, Rajesh Gopakumar, R. Loganayagam, Gautam Mandal, Shiraz Minwalla, Suvrat Raju, Sandip Trivedi and Spenta Wadia DATE : 21 May 2018 to 02 June 2018 VENUE : Ramanujan Lecture Hall, ICTS Bangalore In the past twenty years, the discovery of the AdS/C
From playlist AdS/CFT at 20 and Beyond

Minimal surfaces in R^3 and Maximal surfaces in L^3 (Lecture 2) by Pradip Kumar
ORGANIZERS : C. S. Aravinda and Rukmini Dey DATE & TIME : 16 June 2018 to 25 June 2018 VENUE : Madhava Lecture Hall, ICTS, Bangalore This workshop on geometry and topology for lecturers is aimed for participants who are lecturers in universities/institutes and colleges in India. This w
From playlist Geometry and Topology for Lecturers

Barcodes for Hamiltonian homeomorphisms of surfaces -Benoît Joly
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Topic: Barcodes for Hamiltonian homeomorphisms of surfaces Speaker: Benoît Joly Affiliation: Ruhr-Universität Bochum Date: March 25, 2022 In this talk, we will study the Floer Homology barcodes from a dynamical poin
From playlist Mathematics

How do you find the volume of a sphere
👉 Learn how to find the volume and the surface area of a sphere. A sphere is a perfectly round 3-dimensional object. It is an object with the shape of a round ball. The distance from the center of a sphere to any point on its surface is called the radius of the sphere. A sphere has a unifo
From playlist Volume and Surface Area

An invitation to higher Teichmüller theory – Anna Wienhard – ICM2018
Geometry Invited Lecture 5.11 An invitation to higher Teichmüller theory Anna Wienhard Abstract: Riemann surfaces are of fundamental importance in many areas of mathematics and theoretical physics. The study of the moduli space of Riemann surfaces of a fixed topological type is intimatel
From playlist Geometry