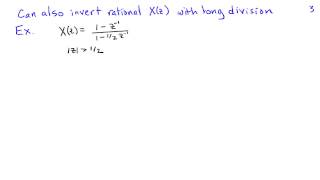Control theory | Filter theory
Matched Z-transform method
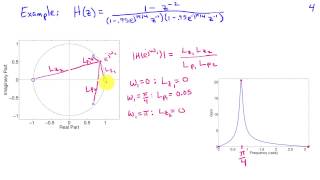
The matched Z-transform method, also called the pole–zero mapping or pole–zero matching method, and abbreviated MPZ or MZT, is a technique for converting a continuous-time filter design to a discrete-time filter (digital filter) design. The method works by mapping all poles and zeros of the s-plane design to z-plane locations , for a sample interval . So an analog filter with transfer function: is transformed into the digital transfer function The gain must be adjusted to normalize the desired gain, typically set to match the analog filter's gain at DC by setting and and solving for . Since the mapping wraps the s-plane's axis around the z-plane's unit circle repeatedly, any zeros (or poles) greater than the Nyquist frequency will be mapped to an aliased location. In the (common) case that the analog transfer function has more poles than zeros, the zeros at may optionally be shifted down to the Nyquist frequency by putting them at , causing the transfer function to drop off as in much the same manner as with the bilinear transform (BLT). While this transform preserves stability and minimum phase, it preserves neither time- nor frequency-domain response and so is not widely used. More common methods include the BLT and impulse invariance methods. MZT does provide less high frequency response error than the BLT, however, making it easier to correct by adding additional zeros, which is called the MZTi (for "improved"). A specific application of the matched Z-transform method in the digital control field is with the Ackermann's formula, which changes the poles of the controllable system; in general from an unstable (or nearby) location to a stable location. (Wikipedia).