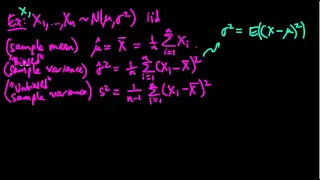
Definition of an estimator. Examples of estimators. Definition of an unbiased estimator.
From playlist Machine Learning

(ML 17.3) Monte Carlo approximation
From playlist Machine Learning

EstimatingRegressionCoefficients.1.EstimatingResidualVariance
This video is brought to you by the Quantitative Analysis Institute at Wellesley College. The material is best viewed as part of the online resources that organize the content and include questions for checking understanding: https://www.wellesley.edu/qai/onlineresources
From playlist Estimating Regression Coefficients

The method of determining eigenvalues as part of calculating the sets of solutions to a linear system of ordinary first-order differential equations.
From playlist A Second Course in Differential Equations
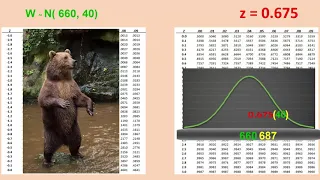
Determining values of a variable at a particular percentile in a normal distribution
From playlist Unit 2: Normal Distributions
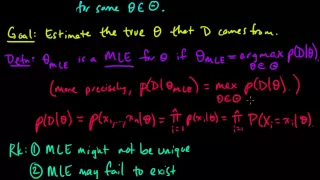
(ML 4.1) Maximum Likelihood Estimation (MLE) (part 1)
Definition of maximum likelihood estimates (MLEs), and a discussion of pros/cons. A playlist of these Machine Learning videos is available here: http://www.youtube.com/my_playlists?p=D0F06AA0D2E8FFBA
From playlist Machine Learning

C07 Homogeneous linear differential equations with constant coefficients
An explanation of the method that will be used to solve for higher-order, linear, homogeneous ODE's with constant coefficients. Using the auxiliary equation and its roots.
From playlist Differential Equations

(ML 7.7.A2) Expectation of a Dirichlet random variable
How to compute the expected value of a Dirichlet distributed random variable.
From playlist Machine Learning

Sequential Stopping for Parallel Monte Carlo by Peter W Glynn
PROGRAM: ADVANCES IN APPLIED PROBABILITY ORGANIZERS: Vivek Borkar, Sandeep Juneja, Kavita Ramanan, Devavrat Shah, and Piyush Srivastava DATE & TIME: 05 August 2019 to 17 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Applied probability has seen a revolutionary growth in resear
From playlist Advances in Applied Probability 2019

Reconstruction and estimation in data driven state-space models- Monbet - Workshop 2 - CEB T3 2019
Monbet (U Rennes, FR) / 15.11.2019 Reconstruction and estimation in data driven state-space models ---------------------------------- Vous pouvez nous rejoindre sur les réseaux sociaux pour suivre nos actualités. Facebook : https://www.facebook.com/InstitutHenriPoincare/ Twitter
From playlist 2019 - T3 - The Mathematics of Climate and the Environment

Kurt Johansson (KTH) -- Multivariate normal approximation for traces of random unitary matrices
Consider an n x n random unitary matrix U taken with respect to normalized Haar measure. It is a well known consequence of the strong Szego limit theorem that the traces of powers of U converge to independent complex normal random variables as n grows. I will discuss a recent result where
From playlist Integrable Probability Working Group

Kalman filtering - Lakshmivarahan
PROGRAM: Data Assimilation Research Program Venue: Centre for Applicable Mathematics-TIFR and Indian Institute of Science Dates: 04 - 23 July, 2011 DESCRIPTION: Data assimilation (DA) is a powerful and versatile method for combining observational data of a system with its dynamical mod
From playlist Data Assimilation Research Program

HTE: Confounding-Robust Estimation
Professor Stefan Wager discusses general principles for the design of robust, machine learning-based algorithms for treatment heterogeneity in observational studies, as well as the application of these principles to design more robust causal forests (as implemented in GRF).
From playlist Machine Learning & Causal Inference: A Short Course

Uncertainty propagation b: Sample estimates
(C) 2012-2013 David Liao (lookatphysics.com) CC-BY-SA Standard deviation vs. sample standard deviation Mean vs. sample mean Standard deviation of the mean vs. standard error of the mean Rule of thumb for thinking about whether error bars overlap
From playlist Probability, statistics, and stochastic processes

Keith Ball: Restricted Invertibility
Keith Ball (University of Warwick) Restricted Invertibility I will briefly discuss the Kadison-Singer problem and then explain a beautiful argument of Bourgain and Tzafriri that I included in an article commissioned in memory of Jean Bourgain.
From playlist Trimester Seminar Series on the Interplay between High-Dimensional Geometry and Probability

Simple Linear Regression (Part E)
Regression Analysis by Dr. Soumen Maity,Department of Mathematics,IIT Kharagpur.For more details on NPTEL visit http://nptel.ac.in
From playlist IIT Kharagpur: Regression Analysis | CosmoLearning.org Mathematics

How optimization for machine learning works, part 2
Part of the End-to-End Machine Learning School course library at http://e2eml.school See these concepts used in an End to End Machine Learning project: https://end-to-end-machine-learning.teachable.com/p/polynomial-regression-optimization/ Watch the rest of the How Optimization Works seri
From playlist E2EML 173. How Optimization for Machine Learning Works

(ML 16.7) EM for the Gaussian mixture model (part 1)
Applying EM (Expectation-Maximization) to estimate the parameters of a Gaussian mixture model. Here we use the alternate formulation presented for (unconstrained) exponential families.
From playlist Machine Learning