Location testing for Gaussian scale mixture distributions

Statistical tests

In statistics, the topic of location testing for Gaussian scale mixture distributions arises in some particular types of situations where the more standard Student's t-test is inapplicable. Specifically, these cases allow tests of location to be made where the assumption that sample observations arise from populations having a normal distribution can be replaced by the assumption that they arise from a Gaussian scale mixture distribution. The class of Gaussian scale mixture distributions contains all symmetric stable distributions, Laplace distributions, logistic distributions, and exponential power distributions, etc. Introduce tGn(x), the counterpart of Student's t-distribution for Gaussian scale mixtures. This means that if we test the null hypothesis that the center of a Gaussian scale mixture distribution is 0, say, then tnG(x) (x ≥ 0) is the infimum of all monotone nondecreasing functions u(x) ≥ 1/2, x ≥ 0 such that if the critical values of the test are u−1(1 − α), then the significance level is at most α ≥ 1/2 for all Gaussian scale mixture distributions [tGn(x) = 1 − tGn(−x),for x < 0]. An explicit formula for tGn(x), is given in the papers in the references in terms of Student’s t-distributions, tk, k = 1, 2, …, n. Introduce ΦG(x):= limn → ∞ tGn(x), the Gaussian scale mixture counterpart of the standard normal cumulative distribution function, Φ(x). Theorem. ΦG(x) = 1/2 for 0 ≤ x < 1, ΦG(1) = 3/4, ΦG(x) = C(x/(2 − x2)1/2) for quantiles between 1/2 and 0.875, where C(x) is the standard Cauchy cumulative distribution function. This is the convex part of the curve ΦG(x), x ≥ 0 which is followed by a linear section ΦG(x) = x/(2√3) + 1/2 for 1.3136… < x < 1.4282... Thus the 90% quantile is exactly 4√3/5. Most importantly, ΦG(x) = Φ(x) for x ≥ √3. Note that Φ(√3) = 0.958…, thus the classical 95% confidence interval for the unknown expected value of Gaussian distributions covers the center of symmetry with at least 95% probability for Gaussian scale mixture distributions. On the other hand, the 90% quantile of ΦG(x) is 4√3/5 = 1.385… > Φ−1(0.9) = 1.282… The following critical values are important in applications: 0.95 = Φ(1.645) = ΦG(1.651), and 0.9 = Φ(1.282) = ΦG(1.386). For the extension of the Theorem to all symmetric unimodal distributions one can start with a classical result of Aleksandr Khinchin: namely that all symmetric unimodal distributions are scale mixtures of symmetric uniformdistributions. (Wikipedia).

(ML 16.7) EM for the Gaussian mixture model (part 1)

Applying EM (Expectation-Maximization) to estimate the parameters of a Gaussian mixture model. Here we use the alternate formulation presented for (unconstrained) exponential families.

From playlist Machine Learning

Mixture Models 4: multivariate Gaussians

Full lecture: http://bit.ly/EM-alg We generalise the equations for the case of a multivariate Gaussians. The main difference from the previous video (part 2) is that instead of a scalar variance we now estimate a covariance matrix, using the same posteriors as before.

From playlist Mixture Models

Mixture Models 3: multivariate Gaussians

From playlist Mixture Models

(ML 16.6) Gaussian mixture model (Mixture of Gaussians)

Introduction to the mixture of Gaussians, a.k.a. Gaussian mixture model (GMM). This is often used for density estimation and clustering.

From playlist Machine Learning

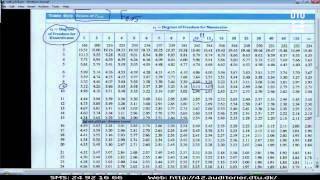
Lect.8G: Hypothesis Test For Two Variances, Example, R And The Numbers Of The Day Example

Example. Lecture with Per B. Brockhoff. Chapters: 00:00 - Example; 10:30 - Software R;

From playlist DTU: Introduction to Statistics | CosmoLearning.org

Multivariate Gaussian distributions

Properties of the multivariate Gaussian probability distribution

From playlist cs273a

(PP 6.3) Gaussian coordinates does not imply (multivariate) Gaussian

An example illustrating the fact that a vector of Gaussian random variables is not necessarily (multivariate) Gaussian.

From playlist Probability Theory

Michael Bertolacci - AdaptSPEC-X: Spectral analysis of multiple non stationary time series

Dr Michael Bertolacci (University of Wollongong) presents “AdaptSPEC-X: Spectral analysis of multiple non stationary time series”, 08/10/2020. Seminar organised by ANU.

From playlist Statistics Across Campuses

Robust and accurate inference via a mixture of Gaussian and terrors by Hyungsuk Tak

20 March 2017 to 25 March 2017 VENUE: Madhava Lecture Hall, ICTS, Bengaluru This joint program is co-sponsored by ICTS and SAMSI (as part of the SAMSI yearlong program on Astronomy; ASTRO). The primary goal of this program is to further enrich the international collaboration in the area

From playlist Time Series Analysis for Synoptic Surveys and Gravitational Wave Astronomy

Didong Li

From playlist Plenary talks One World Symposium 2020

Hypothesis Test: Two Population Proportions

This video explains how to conduct a hypothesis test on two population proportions. http://mathispower4u.com

From playlist Hypothesis Test with Two Samples

Pierre Vandekerkhove: Two-sample contamination model test

CONFERENCE Recording during the thematic meeting : "MLISTRAL" the September 27, 2022 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathem

From playlist Probability and Statistics

Ik Siong Heng - Gaussian Mixture Models for transient gravitational wave detection - IPAM at UCLA

Recorded 29 November 2021. Ik Siong Heng of the University of Glasgow prsents "Gaussian Mixture Models for transient gravitational wave detection" at IPAM's Workshop IV: Big Data in Multi-Messenger Astrophysics. Abstract: The data from the gravitational wave detectors are non-stationary an

From playlist Workshop: Big Data in Multi-Messenger Astrophysics

Gaussian/Normal Distributions

In this video we discuss the Gaussian (AKA Normal) probability distribution function. We show how it relates to the error function (erf) and discuss how to use this distribution analytically and numerically (for example when analyzing real-life sensor data or performing simulation of stoc

From playlist Probability

Efficiently Learning Mixtures of Gaussians - Ankur Moitra

Efficiently Learning Mixtures of Gaussians Ankur Moitra Massachusetts Institute of Technology January 18, 2011 Given data drawn from a mixture of multivariate Gaussians, a basic problem is to accurately estimate the mixture parameters. We provide a polynomial-time algorithm for this proble

From playlist Mathematics

Bayesian Modeling of Behavior (Tutorial) by Konrad Kording

PROGRAM ICTP-ICTS WINTER SCHOOL ON QUANTITATIVE SYSTEMS BIOLOGY (ONLINE) ORGANIZERS: Vijaykumar Krishnamurthy (ICTS-TIFR, India), Venkatesh N. Murthy (Harvard University, USA), Sharad Ramanathan (Harvard University, USA), Sanjay Sane (NCBS-TIFR, India) and Vatsala Thirumalai (NCBS-TIFR,

From playlist ICTP-ICTS Winter School on Quantitative Systems Biology (ONLINE)

Unsupervised Learning

From playlist Machine Learning Course

Statistical Rethinking - Lecture 13

Lecture 13 - Generalized Linear Models (intro) - Statistical Rethinking: A Bayesian Course with R Examples

From playlist Statistical Rethinking Winter 2015

(ML 7.10) Posterior distribution for univariate Gaussian (part 2)

Computing the posterior distribution for the mean of the univariate Gaussian, with a Gaussian prior (assuming known prior mean, and known variances). The posterior is Gaussian, showing that the Gaussian is a conjugate prior for the mean of a Gaussian.

From playlist Machine Learning

Lecture 10B : Mixtures of Experts

Neural Networks for Machine Learning by Geoffrey Hinton [Coursera 2013] Lecture 10B : Mixtures of Experts

From playlist Neural Networks for Machine Learning by Professor Geoffrey Hinton [Complete]

Location testing for Gaussian scale mixture distributions

Related pages