
What are the names of different types of polygons based on the number of sides
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons
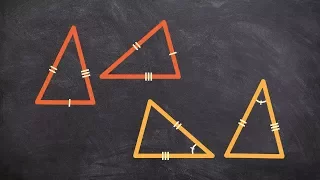
What is an Included Angle - Congruent Triangles
👉 Learn about the included angles of a triangle. An included angle of a triangle is the angle between two sides of a triangle. An included side of a triangle is the side between two angles. To show that two triangles are congruent by the side angle side (SAS) congruency theorem, we must s
From playlist Congruent Triangles

👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties

👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What is the difference between convex and concave
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Tobias EKHOLM - 3/3 Knot contact homology, Chern-Simons theory, and topological string
We explain how knot contact homology is related to the physical theories mentioned in the title. We report on recent progress developing symplectic field theory beyond genus 0 and how this relates to topological strings and open Gromov-Witten invariants. 16 juillet 2015
From playlist 2015 Summer School on Moduli Problems in Symplectic Geometry

👉 Learn how to define and classify different angles based on their characteristics and relationships are given a diagram. The different types of angles that we will discuss will be acute, obtuse, right, adjacent, vertical, supplementary, complementary, and linear pair. The relationships
From playlist Angle Relationships From a Figure

What is a perpendicular bisector
👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties

A Riemann-Roch theorem in Bott-Chern cohomology - Jean-Michel Bismut
Jean-Michel Bismut Université Paris-Sud April 21, 2014 If MM is a complex manifold, the Bott-Chern cohomology H(⋅,⋅)BC(M,C)HBC(⋅,⋅)(M,C) of MM is a refinement of de Rham cohomology, that takes into account the p,q p,q grading of smooth differential forms. By results of Bott and Chern, vect
From playlist Mathematics

Cécile Repellin: "Detecting fractional Chern insulators in few-boson systems"
Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021 Workshop II: Tensor Network States and Applications "Detecting fractional Chern insulators in few-boson systems" Cécile Repellin - Centre National de la Recherche Scientifique (CNRS) Abstract: Realizing stron
From playlist Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021

MagLab Theory Winter School 2019: Bogdan A. Bernevig "Theory"
Topic: Topological Quantum Chemistry: Theory The National MagLab held it's seventh Theory Winter School in Tallahassee, FL from January 7th - 11th, 2019.
From playlist 2019 Theory Winter School
PiTP 2015 - "Conformal Field Theory Methods and Effective Field Theory" - Nicholas Read
https://pitp2015.ias.edu/
From playlist 2015 Prospects in Theoretical Physics Program

What are four types of polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

Nezhla Aghaei - Combinatorial Quantisation of Supergroup Chern-Simons Theory
Chern-Simons Theories with gauge super-groups appear naturally in string theory and they possess interesting applications in mathematics, e.g. for the construction of knot and link invariants. In my talk, I will review the framework of combinatorial quantization of Chern Simons theory and
From playlist Workshop on Quantum Geometry

On the semiregularity map of Bloch by Ananyo Dan
Higgs bundles URL: http://www.icts.res.in/program/hb2016 DATES: Monday 21 Mar, 2016 - Friday 01 Apr, 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore DESCRIPTION: Higgs bundles arise as solutions to noncompact analog of the Yang-Mills equation. Hitchin showed that irreducible solutio
From playlist Higgs Bundles

👉 Learn the essential definitions of triangles. A triangle is a polygon with three sides. Triangles are classified on the basis of their angles or on the basis of their side lengths. The classification of triangles on the bases of their angles are: acute, right and obtuse triangles. The cl
From playlist Types of Triangles and Their Properties

The Chern--Ricci flow | Ben Weinkove
This workshop seeks to explore connections between geometric flows and other areas of mathematics and physics. Geometric flows refer to ways in which geometry can be deformed smoothly in time, rather analogous to the way in which the geometry of the surface of a balloon becomes smooth and
From playlist Research Lectures

