
I explore the Euler Characteristic, and prove that it is equal to 2 for any convex polyhedra. I also discuss some cases when it is not equal to 2. FaceBook: https://www.facebook.com/MathProfPierce Twitter: https://twitter.com/MathProfPierce TikTok: https://www.tiktok.com/@professorheather
From playlist Summer of Math Exposition Youtube Videos

This video given Euler's identity, reviews how to derive Euler's formula using known power series, and then verifies Euler's identity with Euler's formula http://mathispower4u.com
From playlist Mathematics General Interest

Andrew Thomas (7/1/2020): Functional limit theorems for Euler characteristic processes
Title: Functional limit theorems for Euler characteristic processes Abstract: In this talk we will present functional limit theorems for an Euler Characteristic process–the Euler Characteristics of a filtration of Vietoris-Rips complexes. Under this setup, the points underlying the simpli
From playlist AATRN 2020

Derive the Auxiliary Equation for a Cauchy-Euler Equation
This video derives the auxiliarly or characteristic equation used to solve a second order Cauchy-Euler differential equation. Site: http://mathispoweru4.com
From playlist Second Order Homogeneous Cauchy-Euler Differential Equations

How to derive Euler's formula using differential equations! Free ebook http://bookboon.com/en/introduction-to-complex-numbers-ebook A somewhat new proof for the famous formula of Euler. Here is the famous formula named after the mathematician Euler. It relates the exponential with cosin
From playlist Intro to Complex Numbers
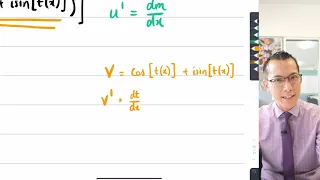
Proving Euler's Formula (2 of 4: Differentiating both sides)
More resources available at www.misterwootube.com
From playlist Introduction to Complex Numbers

Submission for the Summer of Math Exposition (SoME1).
From playlist Summer of Math Exposition Youtube Videos

General Solution to a Second Order Homogeneous Cauchy-Euler Equation (distinct real)
This video provides an example of how to solve a second order homogeneous Cauchy-Euler Equation with the auxiliary equation has two distinct real roots. Site: http://mathispower4u.com
From playlist Second Order Homogeneous Cauchy-Euler Differential Equations

Marc Levine: Refined enumerative geometry (Lecture 3)
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Lecture 3: Virtual fundamental classes in motivic homotopy theory Using the formalism of algebraic stacks, Behrend-Fantechi define the intrinsic normal cone, its fundamental class in
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"
Marc Levine - 2/3 Enumerative Geometry and Quadratic Forms
Notes: https://nextcloud.ihes.fr/index.php/s/9BNtTbXfwAG7xwq Computations of Euler Characteristics and Euler Classes
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Axioms for the fixed point index of an n-valued map
A research talk I gave at KU Leuven Kulak in Kortrijk, Belgium on June 4, 2019, at the conference on Nielsen Theory and Related Topics. The first 20 minutes is mostly about the Euler characteristic, and should be understandable to all mathematicians. The audience was other researchers in t
From playlist Research & conference talks

Differential Equations | Euler Equations Example 2
We solve a second order differential equation known as an Euler equation. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Differential Equations

Richard Thomas - Vafa-Witten Invariants of Projective Surfaces 5/5
This course has 4 sections split over 5 lectures. The first section will be the longest, and hopefully useful for the other courses. 1. Sheaves, moduli and virtual cycles 2. Vafa-Witten invariants: stable and semistable cases 3. Techniques for calculation --- virtual degeneracy loci, cose
From playlist 2021 IHES Summer School - Enumerative Geometry, Physics and Representation Theory
James Arthur - Zeta functions and orbital integrals
We shall review the work of Z. Yun on zeta functions of orders, and of A. Altug on elliptic terms in the trace formula for GL(2). We shall then study the problem of Poisson summation for general linear groups. A suitable solution would be an important step in Langlands' proposed reformula
From playlist Reductive groups and automorphic forms. Dedicated to the French school of automorphic forms and in memory of Roger Godement.

Four theorems about the Euler characteristic and some space invaders
A talk about Euler characteristics and digital topology meant for a general quantitatively literate audience- hopefully understandable to anybody who can handle basic mathematical ideas. I gave this talk at the weekly colloquium for the Fairfield University summer research groups, includin
From playlist Research & conference talks

Representations of (acyclic) quivers, Auslander-Reiten... (Lecture 3) by Laurent Demonet
PROGRAM :SCHOOL ON CLUSTER ALGEBRAS ORGANIZERS :Ashish Gupta and Ashish K Srivastava DATE :08 December 2018 to 22 December 2018 VENUE :Madhava Lecture Hall, ICTS Bangalore In 2000, S. Fomin and A. Zelevinsky introduced Cluster Algebras as abstractions of a combinatoro-algebra
From playlist School on Cluster Algebras 2018

Quasi-hyperbolicity via explicit symmetric (...) - Várilly-Alvarado - Workshop 2 - CEB T2 2019
Anthony Várilly-Alvarado (Rice University) / 26.06.2019 Quasi-hyperbolicity via explicit symmetric differentials. We report on a joint project with Nils Bruin. A surface X is algebraically quasi- hyperbolic if it contains finitely many curves of genus 0 or 1. In 2006, Bogomolov and de O
From playlist 2019 - T2 - Reinventing rational points

Marc Levine: Refined enumerative geometry (Lecture 2)
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Lecture 2: Euler classes, Euler characteristics and Riemann-Hurwicz formulas The Euler class of a vector bundle is defined in the twisted Chow-Witt ring and gives rise to an Euler ch
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Gianmarco Vega-Molino (U Conn) -- Heat Kernel Approach to Index Theorem
We discuss the application of heat kernel approximations to the proof of index theorems on Riemannian manifolds.
From playlist Northeastern Probability Seminar 2020

I define one of the most important constants in mathematics, the Euler-Mascheroni constant. It intuitively measures how far off the harmonic series 1 + 1/2 + ... + 1/n is from ln(n). In this video, I show that the constant must exist. It is an open problem to figure out if the constant is
From playlist Series