
C61 Another problem involving free undamped motion
Another example problem involving damped harmonic motion.
From playlist Differential Equations

A14 Nonhomegeneous linear systems solved by undetermined coefficients
There are two methods for solving nonhomogeneous systems. The first uses undetermined coefficients.
From playlist A Second Course in Differential Equations

C55 Example problem of free undamped motion
Solving a problem of free undamped harmonic motion.
From playlist Differential Equations

Differential Equations | Undetermined Coefficients for a System of DEs
We use the method of undetermined coefficients to solve a nonhomogeneous system of first order linear differential equations. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Systems of Differential Equations

B06 Example problem with separable variables
Solving a differential equation by separating the variables.
From playlist Differential Equations

Transcendental Functions 25 Example problems 2.mp4
Example problems.
From playlist Transcendental Functions
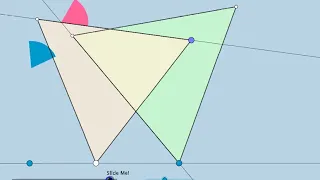
GeoGebra Link: https://www.geogebra.org/m/f5zgupmz
From playlist Geometry: Challenge Problems

B07 Example problem with separable variables
Solving a differential equation by separating the variables.
From playlist Differential Equations
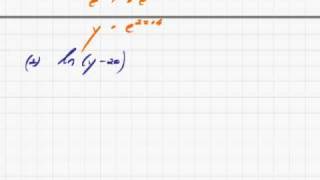
Transcendental Functions 25 Example problems 1.mp4
Example problems.
From playlist Transcendental Functions

Theory of Computation 10. Undecidability and CFLs ADUni
From playlist [Shai Simonson]Theory of Computation

Barry Mazur - Logic, Elliptic curves, and Diophantine stability
This is the first lecture of the 2014 Minerva Lecture series at the Princeton University Mathematics Department October 14, 2014 An introduction to aspects of mathematical logic and the arithmetic of elliptic curves that make these branches of mathematics inspiring to each other. Specif
From playlist Minerva Lectures - Barry Mazur

Turing Meets Paradoxes (History of Undecidability Part 3) - Computerphile
Taking a solemn oath to promise never to write a program that analyses other programs? - That's how Professor Brailsford felt when he first understood undecidability. Latest in our series on the History of Undecidability Undecidability Tangent (History of Undecidability Part 1): http://y
From playlist The History of Undecidability

MIT 18.404J Theory of Computation, Fall 2020 Instructor: Michael Sipser View the complete course: https://ocw.mit.edu/18-404JF20 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP60_JNv2MmK3wkOt9syvfQWY Quickly reviewed last lecture. Showed that natural numbers and real n
From playlist MIT 18.404J Theory of Computation, Fall 2020

Theory of Computation 13. The Halting Problem aduni
From playlist [Shai Simonson]Theory of Computation

Alexandra SHLAPENTOKH - Defining Valuation Rings and Other Definability Problems in Number Theory
We discuss questions concerning first-order and existential definability over number fields and function fields in the language of rings and its extensions. In particular, we consider the problem of defining valuations rings over finite and infinite algebraic extensions
From playlist Mathematics is a long conversation: a celebration of Barry Mazur

Diophantine approximation and Diophantine definitions - Héctor Pastén Vásquez
Short Talks by Postdoctoral Members Héctor Pastén Vásquez - September 29, 2015 http://www.math.ias.edu/calendar/event/88264/1443549600/1443550500 More videos on http://video.ias.edu
From playlist Short Talks by Postdoctoral Members

Are These Batteries The Future Of Energy Storage?
Are These Batteries The Future Of Energy Storage? See why hiring doesn’t have to be difficult — when you try ZipRecruiter for free at https://www.ziprecruiter.com/UNDECIDED. There’s a huge number of lithium-ion battery alternatives in the works … so many that it can be hard to keep track o
From playlist Battery technology

The Truth About Plastic Recycling ... It’s Complicated
The Truth About Plastic Recycling. The first 100 people to use code UNDECIDED at the link below will get 20% off of Incogni: https://incogni.com/undecided Is it a scam? It's complicated. The 3R’s: reduce, reuse, recycle has been drilled into our heads as the way forward towards a sustainab
From playlist The truth about

B05 Example problem with separable variables
Solving a differential equation by separating the variables.
From playlist Differential Equations

Computably enumerable sets and undecidability
In this video we're going to define and implement decidable as well as semidecidable. Code is found under https://gist.github.com/Nikolaj-K/808149debf7c3b09705127f9205f6c3f Other names for the two are recursive or computable resp. recursively enumerable, computably enumerable - I also say
From playlist Programming