
Geometry - Ch. 1: Basic Concepts (28 of 49) What are Convex and Concave Angles?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain how to identify convex and concave polygons. Convex polygon: When extending any line segment (side) it does NOT cut through any of the other sides. Concave polygon: When extending any line seg
From playlist THE "WHAT IS" PLAYLIST

In this video, I talk about convexity, which is the most important concept in applied mathematics. I also give a beautiful application in partial differential equations, more specifically I prove backwards uniqueness of the heat equation. This is based off the famous PDE book by Evans, who
From playlist Partial Differential Equations

Fixed income: Effective Convexity (FRM T4-37)
Effective convexity approximates modified convexity (just as effective duration approximates modified duration). Mathematically, convexity is a function of the bond's second derivative with respect to yield: convexity = 1/P*∂^2P/∂y^2. Convexity is illustrated by the curvature (i.e., non-li
From playlist Valuation and RIsk Models (FRM Topic 4)

Fixed Income: Analytical Convexity; aka, modified convexity (FRM T4-41)
In this video, I will show you how to calculate modified convexity by matching the modified convexity that Tuckman shows in Table 4.6 in Chapter 4 of his book, Fixed Income Securities. 💡 Discuss this video here in our forum: https://trtl.bz/2YBEHeB. 📗 You can find Tuckman's Fixed Income
From playlist Valuation and RIsk Models (FRM Topic 4)

Fixed Income: Duration and Convexity Summary (FRM T4-42)
In this playlist, I've already recorded at least ten videos on duration and convexity which are the two most common measures of single-factor interest rate risk. So, in this video, we wrap it up in one simple explanation that tries to illustrate both duration and convexity and how we apply
From playlist Valuation and RIsk Models (FRM Topic 4)

Convexity and risk premium impacts on shape of term structure (FRM T5-08)
In this video, I'm going to try to illustrate all of the important ideas that are in Tuckman's Chapter 8: The Evolution of Short Rates and the Shape of the Term Structure. This chapter discusses the shape of the term structure and the key influences on the shape of the spot rate term struc
From playlist Market Risk (FRM Topic 5)

Fixed Income: Duration plus convexity to approximate bond price change (FRM T4-38)
Duration plus a convexity adjustment is a good estimate (approximation) of the bond's price change. We can express this change in percentage terms(%) as given by ΔP/P = -D*Δy + 0.5*C*(Δy)^2; or we can express this in dollar terms ($) as given by ΔP =∂P/∂y*Δy + 0.5*∂^2P/∂y^2*(Δy)^2. 💡 Dis
From playlist Valuation and RIsk Models (FRM Topic 4)

Fixed Income: Bullet versus Barbell Bond Portfolio (FRM T4-40)
The bullet portfolio invests in a single medium-term bond. The corresponding barbell portfolio invests the same amount of capital and achieves the same duration, but invests in a mix of the short-term plus long-term bond. But the barbell portfolio will have greater convexity. Tuckman expla
From playlist Valuation and RIsk Models (FRM Topic 4)
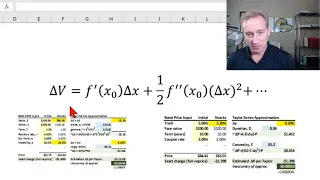
Delta-gamma value at risk (VaR) with the Taylor Series Approximation (FRM T4-4)
[here is my xls https://trtl.bz/2rlVj7H] The Taylor Series lets us approximate a smooth function with a polynomial. Here we apply it to both an option position (where the second term captures gamma) and a bond position (where the second term captures convexity). 💡 Discuss this video here
From playlist Valuation and RIsk Models (FRM Topic 4)

Suvrit Sra: Lecture series on Aspects of Convex, Nonconvex, and Geometric Optimization (Lecture 3)
The lecture was held within the framework of the Hausdorff Trimester Program "Mathematics of Signal Processing". (28.1.2016)
From playlist HIM Lectures: Trimester Program "Mathematics of Signal Processing"

How the portfolio possibilities curve (PPC) illustrates the benefit of diversification (FRM T1-7)
When correlations are imperfect, diversification benefits are possible. The portfolio possibilities curve illustrates this and it contains two notable points: the minimum variance portfolio (MVP) and the optimal portfolio (with the highest Sharpe ratio). At the end, I summarize four featur
From playlist Risk Foundations (FRM Topic 1)

Light and Optics 5_2 Refractive Surfaces
Problems involving refractive surfaces.
From playlist Physics - Light and Optics

In this presentation, Paritosh Mokhasi describes robust optimization, a framework for solving optimization problems in the presence of uncertainties. He covers the concept of robust optimization and how the problems are formulated, showing examples that demonstrate how the new Wolfram Lang
From playlist Wolfram Technology Conference 2020






